If a^2 + b^2 = 4 and c^2 + d^2 = 8, what is ac + bd?

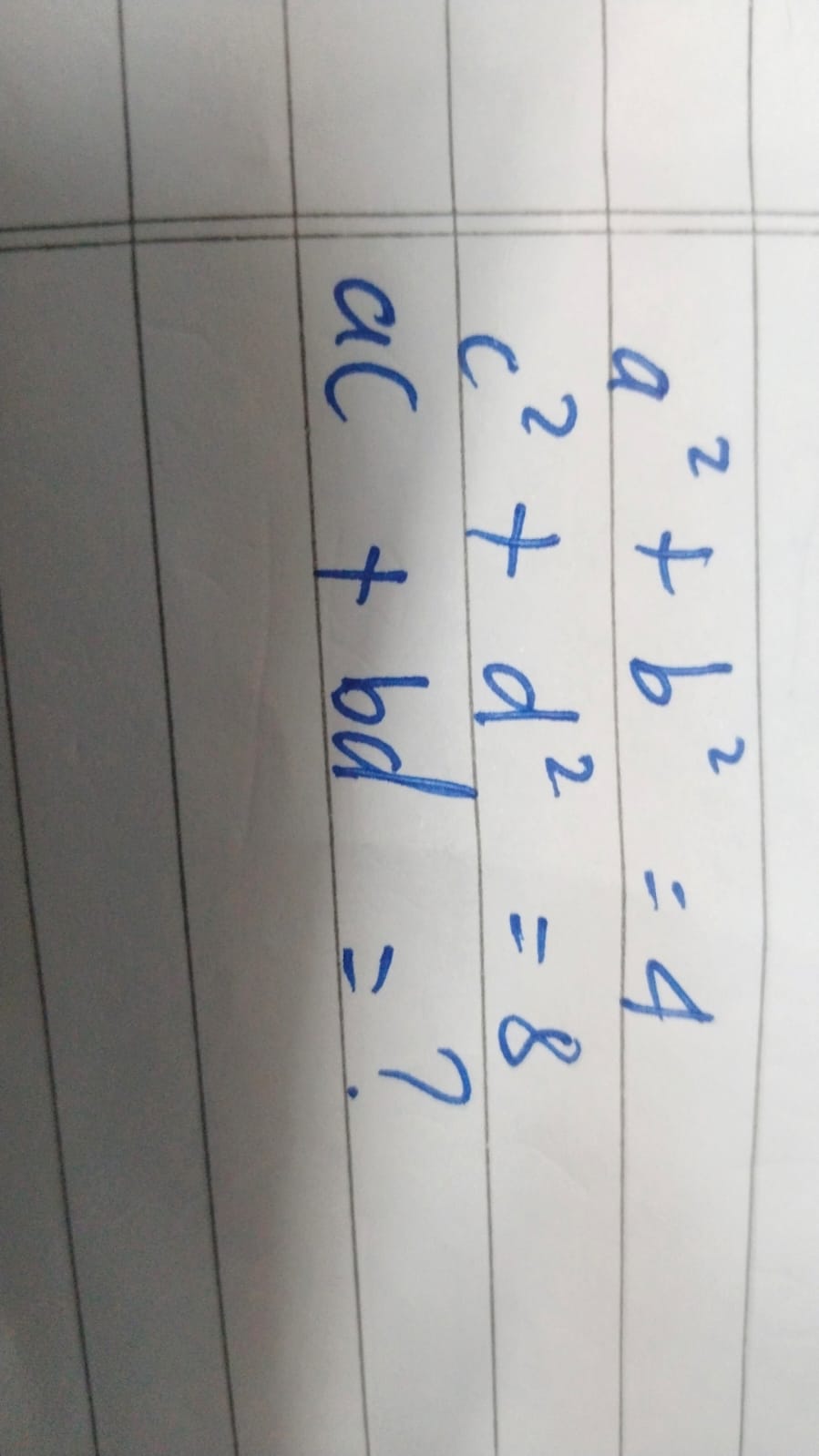
Understand the Problem

The question is asking to find the value of the expression 'ac + bd' given the equations a^2 + b^2 = 4, c^2 + d^2 = 8. This requires applying algebraic techniques possibly related to the identities involving squares and products.

Answer

The maximum value of $ ac + bd $ is $ 4\sqrt{2} $.

Steps to Solve

Use the identity for squares We can use the identity that relates the squares of sums to the products: $$(a + bi)(c + di) = ac + adi + bci - bd$$ From this, we can derive that: $$ a^2 + b^2 = (a + bi)(a - bi) $$
Relate to given equations Given:

( a^2 + b^2 = 4 )
( c^2 + d^2 = 8 )

We want to find the value of ( ac + bd ).

Apply the Cauchy-Schwarz inequality According to the Cauchy-Schwarz inequality, we have: $$(a^2 + b^2)(c^2 + d^2) \geq (ac + bd)^2$$ Substituting the known values: $$(4)(8) \geq (ac + bd)^2$$
Simplify the inequality This simplifies to: $$32 \geq (ac + bd)^2$$
Take square roots Taking the square root of both sides gives: $$ \sqrt{32} \geq |ac + bd| $$ So, we have: $$ ac + bd \leq 4\sqrt{2} $$
Setting maximum condition The maximum value ( ac + bd ) can reach is when the vectors formed by ( (a, b) ) and ( (c, d) ) are parallel. Thus, the best outcome we are looking for from our setup is: $$ ac + bd = 4\sqrt{2} $$

The maximum value of ( ac + bd ) is ( 4\sqrt{2} ).

More Information

The inequality utilized here is related to the concept of dot products in vector spaces. The Cauchy-Schwarz inequality provides a significant insight into the relationship between magnitudes and angles in multi-dimensional spaces.

Tips

Misapplying the Cauchy-Schwarz inequality by ignoring the conditions of equality which would require the vectors to be in the same direction.
Not substituting the given values accurately into the identities or inequalities.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!