If A = { x ∈ R : 4x^2 = 2x + 3 } B = { x ∈ R : log(x^2) = (log(x))^2 } find A ∩ B.
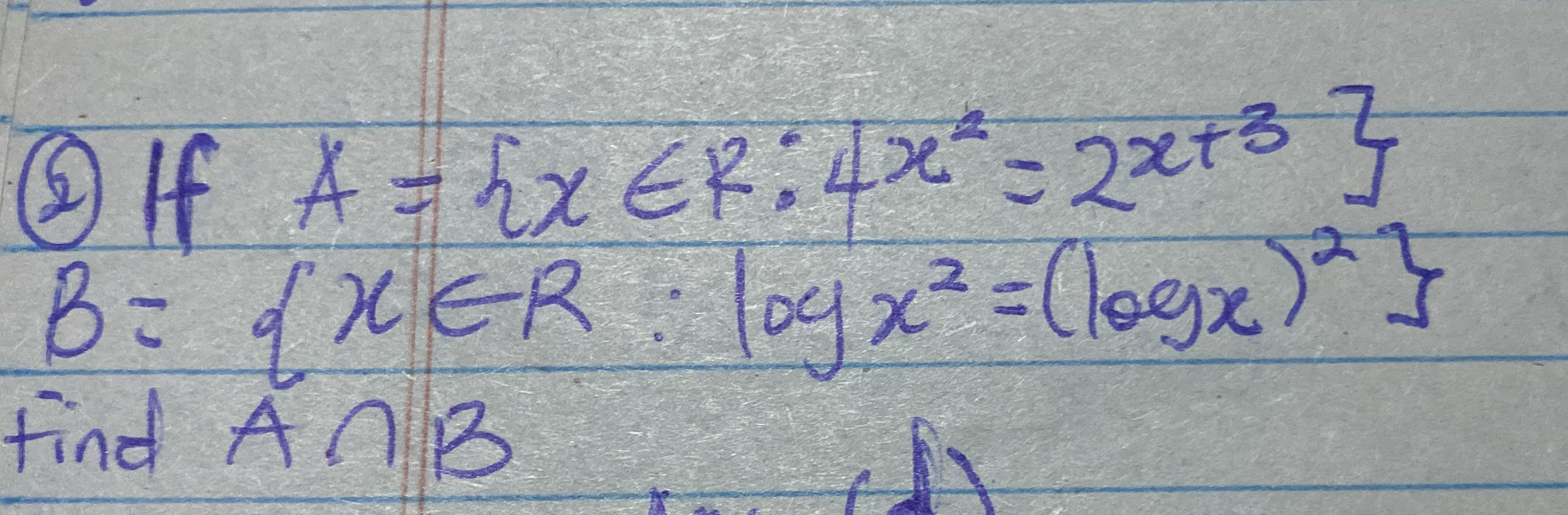
Understand the Problem
The question involves two sets, A and B, defined by certain mathematical expressions, and asks for the intersection of these sets (denoted as A ∩ B). It requires identifying the elements that are common to both sets based on the given conditions.
Answer
The intersection \( A \cap B \) is \( \{ 1 \} \).
Answer for screen readers
The intersection ( A \cap B ) is:
$$ A \cap B = { 1 } $$
Steps to Solve
- Solve for Set A
Starting with the equation $4x^2 = 2x + 3$, we can rearrange it:
$$ 4x^2 - 2x - 3 = 0 $$
Next, we will use the quadratic formula:
$$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$
where ( a = 4, b = -2, c = -3 ).
Calculating the discriminant:
$$ b^2 - 4ac = (-2)^2 - 4(4)(-3) = 4 + 48 = 52 $$
Now substituting back into the formula:
$$ x = \frac{2 \pm \sqrt{52}}{8} $$
Simplifying further gives:
$$ x = \frac{2 \pm 2\sqrt{13}}{8} = \frac{1 \pm \sqrt{13}}{4} $$
Thus, Set A is:
$$ A = \left{ \frac{1 + \sqrt{13}}{4}, \frac{1 - \sqrt{13}}{4} \right} $$
- Solve for Set B
Starting with the equation $log(x^2) = (log(x))^2$, we can rewrite it using properties of logarithms:
$$ 2 \log(x) = (\log(x))^2 $$
Next, letting ( y = \log(x) ), we can rewrite the equation as:
$$ 2y = y^2 $$
Rearranging gives:
$$ y^2 - 2y = 0 \ y(y - 2) = 0 $$
So,
$$ y = 0 \quad \text{or} \quad y = 2 $$
Now substituting back for ( x ):
- If ( y = 0 ), then ( \log(x) = 0 ) implies ( x = 1 ).
- If ( y = 2 ), then ( \log(x) = 2 ) implies ( x = 10^2 = 100 ).
Thus, Set B is:
$$ B = { 1, 100 } $$
- Find the Intersection A ∩ B
Now we find the common elements between Set A and Set B:
Set A has:
$$ A = \left{ \frac{1 + \sqrt{13}}{4}, \frac{1 - \sqrt{13}}{4} \right} $$
Evaluating these values numerically:
- ( \frac{1 + \sqrt{13}}{4} \approx 1.30 )
- ( \frac{1 - \sqrt{13}}{4} \approx -0.30 )
So, Set A approximately contains one element greater than 1 and the other is negative.
Set B has:
$$ B = { 1, 100 } $$
Comparing the elements, we see that:
The only common element is ( 1 ).
The intersection ( A \cap B ) is:
$$ A \cap B = { 1 } $$
More Information
The intersection of two sets consists of elements that are present in both sets. Here, we found out that the value ( 1 ) satisfies both conditions of sets A and B.
Tips
- Confusing the steps in the quadratic formula, such as forgetting to subtract or miscalculating the discriminant.
- Not recognizing the logarithmic properties, leading to incorrect simplifications of the equation.
AI-generated content may contain errors. Please verify critical information