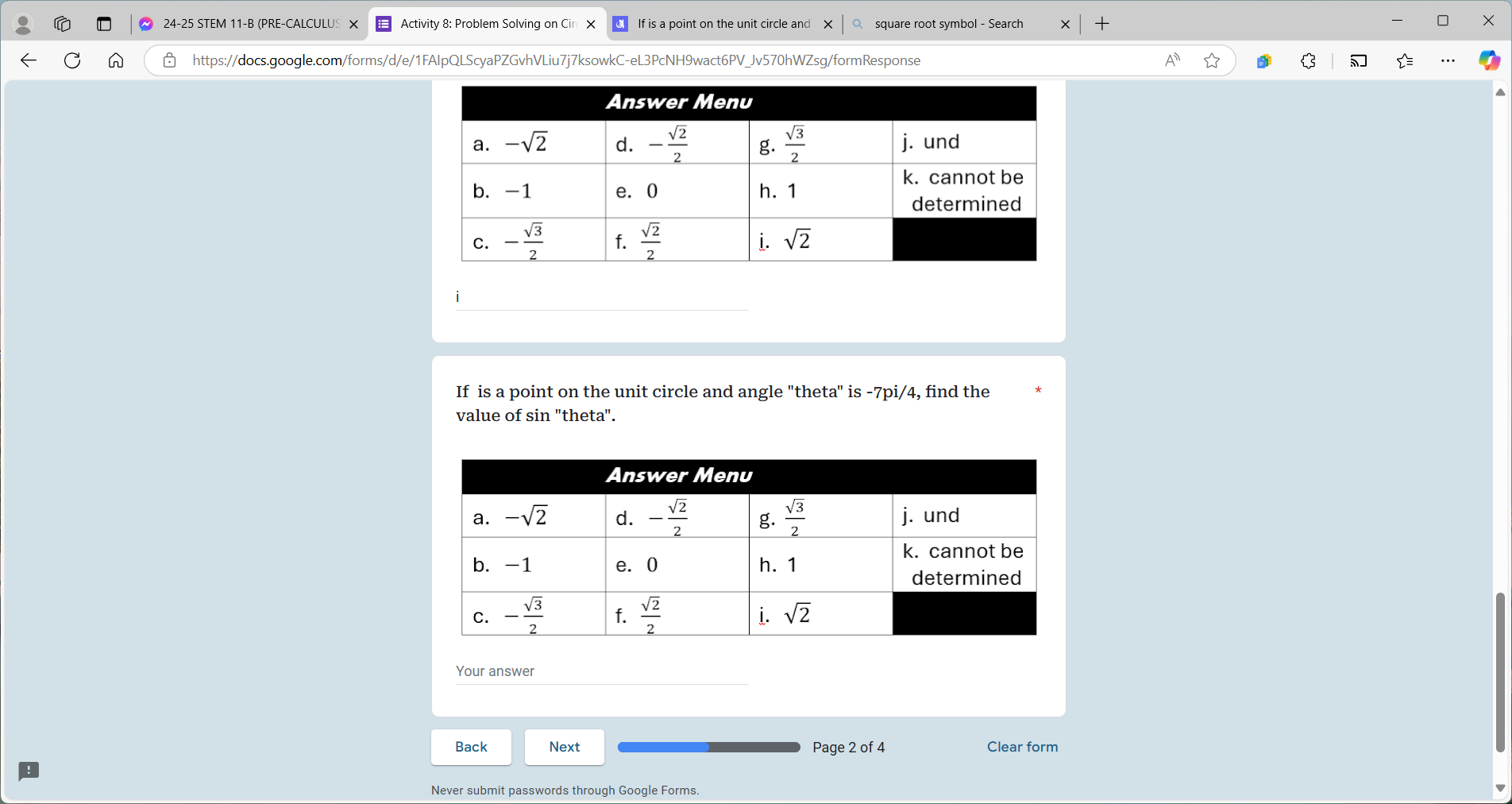
If a point is on the unit circle and angle 'theta' is -7pi/4, find the value of sin(theta).
Understand the Problem
The question is asking to find the value of sin(theta) for the angle -7pi/4, which is located on the unit circle. This involves understanding the position of -7pi/4 on the unit circle and calculating the sine value based on its coordinates.
Answer
The value of $\sin\left(-\frac{7\pi}{4}\right)$ is $\frac{\sqrt{2}}{2}$.
Answer for screen readers
The value of $\sin\left(-\frac{7\pi}{4}\right)$ is $\frac{\sqrt{2}}{2}$.
Steps to Solve
-
Finding the equivalent angle in standard position To find the angle equivalent to $-\frac{7\pi}{4}$ in standard position, add $2\pi$ (which is $8\pi/4$) to $-\frac{7\pi}{4}$: $$ -\frac{7\pi}{4} + 2\pi = -\frac{7\pi}{4} + \frac{8\pi}{4} = \frac{\pi}{4} $$
-
Identifying the coordinates on the unit circle The angle of $\frac{\pi}{4}$ corresponds to the coordinates on the unit circle, which are: $$ \left( \cos\left(\frac{\pi}{4}\right), \sin\left(\frac{\pi}{4}\right) \right) = \left( \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right) $$
-
Finding the sine value Since sine corresponds to the y-coordinate of the point on the unit circle, we have: $$ \sin\left(-\frac{7\pi}{4}\right) = \sin\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2} $$
The value of $\sin\left(-\frac{7\pi}{4}\right)$ is $\frac{\sqrt{2}}{2}$.
More Information
The sine of an angle indicates the y-coordinate of the corresponding point on the unit circle. The angle $-\frac{7\pi}{4}$ is equivalent to $\frac{\pi}{4}$, a commonly encountered angle in trigonometry that provides the sine value of $\frac{\sqrt{2}}{2}$.
Tips
- Not adding $2\pi$ correctly: Make sure to adjust the negative angle by adding the correct amount to find the equivalent positive angle.
- Forgetting the coordinates: Always remember that sine corresponds to the y-coordinate on the unit circle.
AI-generated content may contain errors. Please verify critical information