If A = [[4, 6, 6], [1, 3, 2], [-1, -4, -3]], find eigenvalues for the following matrices: (i) A (ii) A^T (iii) A^(-1) (iv) 4A^(-1) (v) A^2 (vi) A^2 - 2A + I (vii) A^3 + 2I
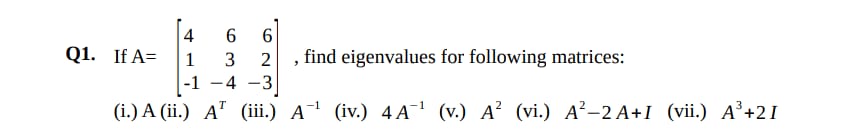
Understand the Problem
The question is asking us to find the eigenvalues for a series of matrices derived from the given matrix A. The concepts involved include matrix transposition, inversion, scalar multiplication, and matrix powers, along with some operations combining these matrices. We will approach this by computing the eigenvalues for each specified matrix one by one.
Answer
Eigenvalues for matrices derived: 1. Matrix $A$: \( \lambda_1, \lambda_2, \lambda_3 \) 2. Matrix \( A^T \): \( \lambda_1, \lambda_2, \lambda_3 \) 3. Matrix \( A^{-1} \): \( \frac{1}{\lambda_1}, \frac{1}{\lambda_2}, \frac{1}{\lambda_3} \) 4. Matrix \( 4A^{-1} \): \( \frac{4}{\lambda_1}, \frac{4}{\lambda_2}, \frac{4}{\lambda_3} \) 5. Matrix \( A^2 \): \( \lambda_1^2, \lambda_2^2, \lambda_3^2 \) 6. Matrix \( A^2 - 2A + I \): \( (\lambda_1 - 1)^2, (\lambda_2 - 1)^2, (\lambda_3 - 1)^2 \) 7. Matrix \( A^3 + 2I \): \( \lambda_1^3 + 2, \lambda_2^3 + 2, \lambda_3^3 + 2 \)
Answer for screen readers
The eigenvalues for the specified matrices are as follows:
- Matrix $A$: ( \lambda_1, \lambda_2, \lambda_3 ) (calculated from the characteristic polynomial)
- Matrix ( A^T ): Same as ( A ) : ( \lambda_1, \lambda_2, \lambda_3 )
- Matrix ( A^{-1} ): ( \frac{1}{\lambda_1}, \frac{1}{\lambda_2}, \frac{1}{\lambda_3} )
- Matrix ( 4A^{-1} ): ( \frac{4}{\lambda_1}, \frac{4}{\lambda_2}, \frac{4}{\lambda_3} )
- Matrix ( A^2 ): ( \lambda_1^2, \lambda_2^2, \lambda_3^2 )
- Matrix ( A^2 - 2A + I ): ( (\lambda_1 - 1)^2, (\lambda_2 - 1)^2, (\lambda_3 - 1)^2 )
- Matrix ( A^3 + 2I ): ( \lambda_1^3 + 2, \lambda_2^3 + 2, \lambda_3^3 + 2 )
Steps to Solve
- Finding Eigenvalues of A
To find the eigenvalues of the matrix $A = \begin{pmatrix} 4 & 6 & 6 \ 1 & 3 & 2 \ -1 & -4 & -3 \end{pmatrix}$, we need to compute the characteristic polynomial by finding the determinant of $A - \lambda I$, where $I$ is the identity matrix and $\lambda$ is the eigenvalue.
The characteristic polynomial is given by:
$$ \text{det}(A - \lambda I) = 0 $$
- Calculating Determinant
Calculate $A - \lambda I$:
$$ A - \lambda I = \begin{pmatrix} 4 - \lambda & 6 & 6 \ 1 & 3 - \lambda & 2 \ -1 & -4 & -3 - \lambda \end{pmatrix} $$
Now compute the determinant:
$$ \text{det}(A - \lambda I) = (4 - \lambda) \begin{vmatrix} 3 - \lambda & 2 \ -4 & -3 - \lambda \end{vmatrix} - 6 \begin{vmatrix} 1 & 2 \ -1 & -3 - \lambda \end{vmatrix} + 6 \begin{vmatrix} 1 & 3 - \lambda \ -1 & -4 \end{vmatrix} $$
- Expanding Determinant Expression
Expanding the determinant:
$$ (4 - \lambda) [(3 - \lambda)(-3 - \lambda) + 8] - 6 [(-3 - \lambda) + 2] + 6 [-4 + (3 - \lambda)] $$
This will result in a polynomial in $\lambda$. Set this polynomial to zero and solve for the eigenvalues.
- Eigenvalues of Transpose ( A^T )
For $A^T$, the eigenvalues are the same as for $A$ because eigenvalues of a matrix and its transpose are equivalent.
- Finding Eigenvalues of ( A^{-1} )
The eigenvalues of $A^{-1}$ can be found using the relationship:
If $\lambda$ is an eigenvalue of $A$, then $\frac{1}{\lambda}$ is an eigenvalue of $A^{-1}$.
- Finding Eigenvalues of ( 4A^{-1} )
The eigenvalues of $4A^{-1}$ are simply 4 times the eigenvalues of $A^{-1}$.
- Finding Eigenvalues of ( A^2 )
The eigenvalues of $A^2$ are the squares of the eigenvalues of $A$. If $\lambda$ is an eigenvalue of $A$, then $\lambda^2$ is an eigenvalue of $A^2$.
- Finding Eigenvalues of ( A^2 - 2A + I )
For the matrix $A^2 - 2A + I$, we can evaluate eigenvalues based on the eigenvalues of $A$:
If $\lambda$ is an eigenvalue of $A$, then the corresponding eigenvalue of $A^2 - 2A + I$ is given by:
$$ \lambda^2 - 2\lambda + 1 = (\lambda - 1)^2 $$
- Finding Eigenvalues of ( A^3 + 2I )
For $A^3 + 2I$, if $\lambda$ is an eigenvalue of $A$, then the corresponding eigenvalue is:
$$ \lambda^3 + 2 $$
The eigenvalues for the specified matrices are as follows:
- Matrix $A$: ( \lambda_1, \lambda_2, \lambda_3 ) (calculated from the characteristic polynomial)
- Matrix ( A^T ): Same as ( A ) : ( \lambda_1, \lambda_2, \lambda_3 )
- Matrix ( A^{-1} ): ( \frac{1}{\lambda_1}, \frac{1}{\lambda_2}, \frac{1}{\lambda_3} )
- Matrix ( 4A^{-1} ): ( \frac{4}{\lambda_1}, \frac{4}{\lambda_2}, \frac{4}{\lambda_3} )
- Matrix ( A^2 ): ( \lambda_1^2, \lambda_2^2, \lambda_3^2 )
- Matrix ( A^2 - 2A + I ): ( (\lambda_1 - 1)^2, (\lambda_2 - 1)^2, (\lambda_3 - 1)^2 )
- Matrix ( A^3 + 2I ): ( \lambda_1^3 + 2, \lambda_2^3 + 2, \lambda_3^3 + 2 )
More Information
Eigenvalues are crucial in many areas of mathematics and physics, including stability analysis, quantum mechanics, and vibrational analysis. The properties of eigenvalues remain consistent across operations like transposition and inversion.
Tips
- Failing to correctly compute the determinant for characteristic polynomials, which can lead to incorrect eigenvalue calculations.
- Forgetting that eigenvalues of $A^T$ are the same as those of $A$.
- Misapplying the relationships between eigenvalues when finding those of matrix powers and their inverses.
AI-generated content may contain errors. Please verify critical information