If A = {4, 5, 8, 12}, B = {1, 4, 6, 9} and C = {1, 2, 3, 4}, then find (i) A - (B - A) (ii) A - (C - B).

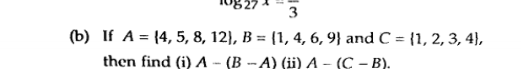
Understand the Problem

The question is asking us to perform set operations involving three sets A, B, and C. Specifically, it asks for the results of the operations A minus (B minus A) and A minus (C minus B). This requires an understanding of basic set theory.

Answer

(i) $ \{4, 5, 8, 12\} $; (ii) $ \{4, 5, 8, 12\} $

Steps to Solve

Calculate B - A
To find ( B - A ), we identify the elements in set B that are not in set A. $$ B = {1, 4, 6, 9} $$ $$ A = {4, 5, 8, 12} $$ Elements in B that are not in A:
( B - A = {1, 6, 9} )
Calculate A - (B - A)
Now we need to find ( A - (B - A) ), which means we will subtract the elements of ( B - A ) from A. $$ A = {4, 5, 8, 12} $$ $$ B - A = {1, 6, 9} $$ Elements in A that are not in ( B - A ):
( A - (B - A) = {4, 5, 8, 12} )
Calculate C - B
Next, we find ( C - B ), which is the set of elements in C that are not in B. $$ C = {1, 2, 3, 4} $$ $$ B = {1, 4, 6, 9} $$ Elements in C that are not in B:
( C - B = {2, 3} )
Calculate A - (C - B)
Finally, we calculate ( A - (C - B) ) by subtracting the elements of ( C - B ) from A. $$ A = {4, 5, 8, 12} $$ $$ C - B = {2, 3} $$ Elements in A that are not in ( C - B ):
( A - (C - B) = {4, 5, 8, 12} )

(i) ( A - (B - A) = {4, 5, 8, 12} )

(ii) ( A - (C - B) = {4, 5, 8, 12} )

More Information

Both operations yield the same result, which means that the elements in A are not affected by the elements removed from sets B and C. This indicates that all elements of A are present regardless of the subtractions made by B and C.

Tips

Confusing the operation ( B - A ) with ( A - B ). It's important to remember that the first set is being reduced by elements in the second.
Misinterpreting the empty set. If a set has no elements left after subtraction, the result is empty, which should be stated clearly.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!