( (i - 1) / (i^2) )^2 (i + 1) = ?
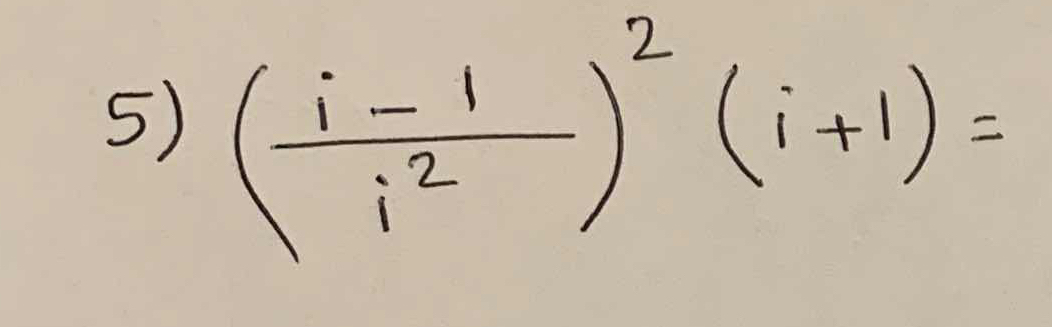
Understand the Problem
The question involves simplifying or solving the expression that contains complex numbers, specifically involving 'i', which is the imaginary unit. The task is likely to simplify the left side of the equation and equate it to the right side.
Answer
The result is \( 2 - 2i \).
Answer for screen readers
The final result is ( 2 - 2i ).
Steps to Solve
- Calculate ( i^2 )
The imaginary unit ( i ) is defined as ( i = \sqrt{-1} ). Therefore, we have: $$ i^2 = -1 $$
- Substitute ( i^2 ) into the expression
Replace ( i^2 ) in the expression: $$ \left( \frac{i - 1}{i^2} \right)^2 (i + 1) = \left( \frac{i - 1}{-1} \right)^2 (i + 1) $$
- Simplify the fraction
Simplifying ( \frac{i - 1}{-1} ): $$ \frac{i - 1}{-1} = -i + 1 = 1 - i $$
- Square the simplified expression
Now square ( (1 - i) ): $$ (1 - i)^2 = 1^2 - 2(1)(i) + i^2 = 1 - 2i - 1 = -2i $$
- Combine with ( (i + 1) )
Now multiply the squared result with ( (i + 1) ): $$ -2i(i + 1) = -2i^2 - 2i = -2(-1) - 2i = 2 - 2i $$
The final result is ( 2 - 2i ).
More Information
The expression involves the manipulation of complex numbers, particularly squaring expressions, applying the definition of ( i ), and simplifying calculations to arrive at a solution.
Tips
- Forgetting the definition of ( i^2 ) and assuming it is a real number.
- Overlooking the need to square both the real and imaginary parts in ( (1 - i)^2 ).
- Confusing the order of operations when simplifying complex multiplications.
AI-generated content may contain errors. Please verify critical information