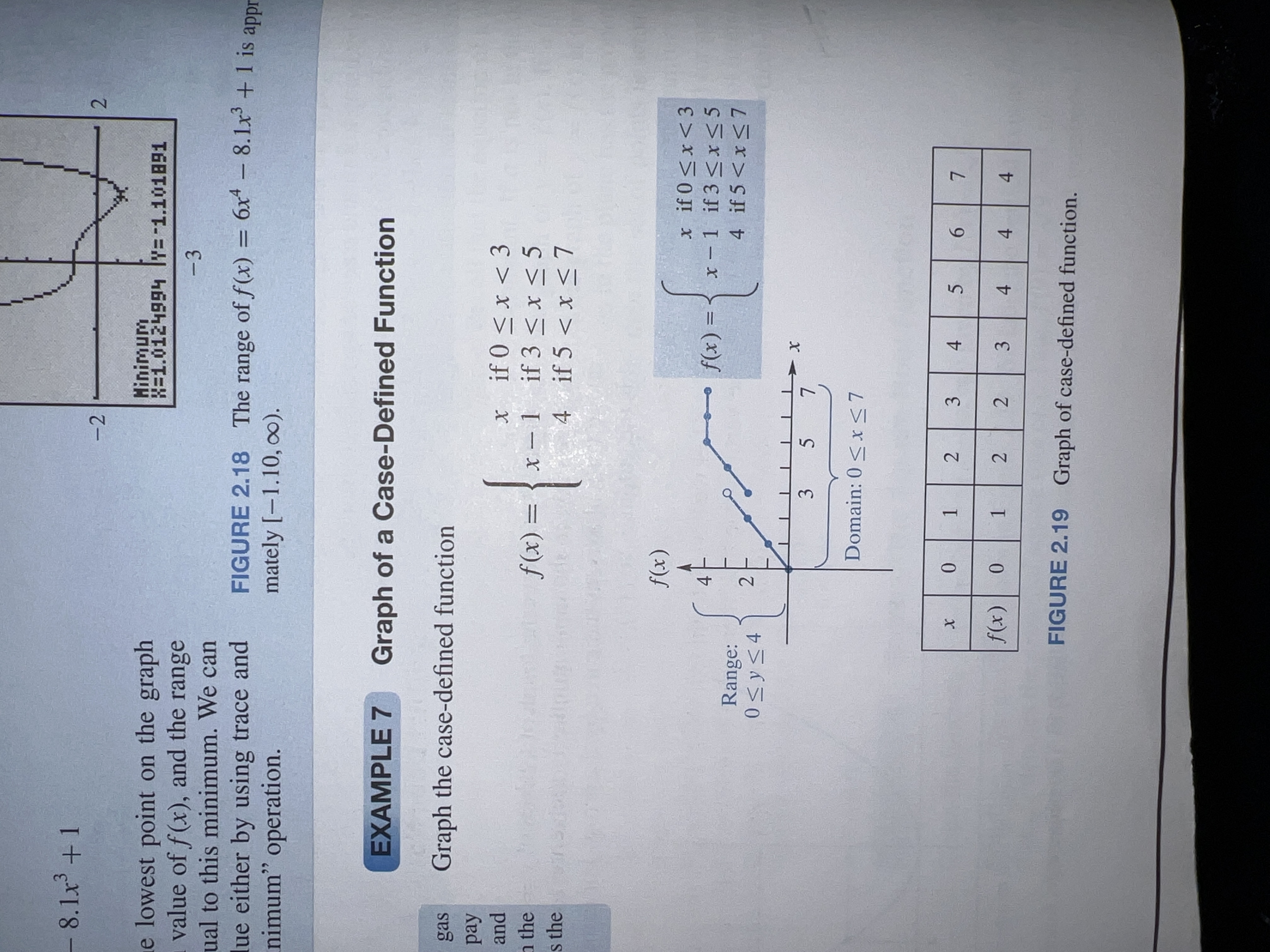
Graph the case-defined function f(x) = { x if 0 ≤ x < 3; x - 1 if 3 ≤ x ≤ 5; 4 if 5 < x ≤ 7 }.
Understand the Problem
The question is asking to graph a piecewise function defined in different intervals. We need to represent the function based on its defined cases, showing the domain and range of values.
Answer
The domain of the function is \( [0, 7] \) and the range is \( [0, 4] \).
Answer for screen readers
The graph of the piecewise function ( f(x) ) is shown as composed of three segments. The overall domain is ( [0, 7] ) and the overall range is ( [0, 4] ).
Steps to Solve
- Identify the cases of the function
The function ( f(x) ) is defined as follows:
- ( f(x) = x ) if ( 0 \leq x < 3 )
- ( f(x) = x - 1 ) if ( 3 \leq x < 5 )
- ( f(x) = 4 ) if ( 5 \leq x \leq 7 )
- Graph the first case
For the interval ( [0, 3) ):
- Start plotting points:
- ( f(0) = 0 )
- ( f(1) = 1 )
- ( f(2) = 2 )
- ( f(3) = 3 ) (this point will not be closed because of the open interval at 3)
- Graph the second case
For the interval ( [3, 5) ):
- Start plotting points:
- ( f(3) = 3 - 1 = 2 ) (this point will be closed)
- ( f(4) = 4 - 1 = 3 )
- ( f(5) = 5 - 1 = 4 ) (this point will not be closed because of the open interval at 5)
- Graph the third case
For the interval ( [5, 7] ):
- The function is constant at ( f(x) = 4 ) for this interval.
- Thus, plot:
- ( f(5) = 4 ) (this point will be closed)
- ( f(6) = 4 )
- ( f(7) = 4 ) (this point will also be closed)
- Label the axes and provide the range and domain
- The x-axis (domain) ranges from ( 0 ) to ( 7 ).
- The y-axis (range) ranges from ( 0 ) to ( 4 ).
The graph of the piecewise function ( f(x) ) is shown as composed of three segments. The overall domain is ( [0, 7] ) and the overall range is ( [0, 4] ).
More Information
The function ( f(x) ) is defined in a piecewise manner, which means different expressions apply to different ranges of ( x ). This type of function is common in situations where outputs change based on input conditions, often seen in real-world scenarios like tax brackets or shipping cost calculations.
Tips
- Forgetting to use open or closed circles on the graph, which is crucial for indicating whether certain endpoints are included in the intervals.
- Not understanding the transitions between cases; ensuring clarity in intervals is important to define where each case starts and ends.
AI-generated content may contain errors. Please verify critical information