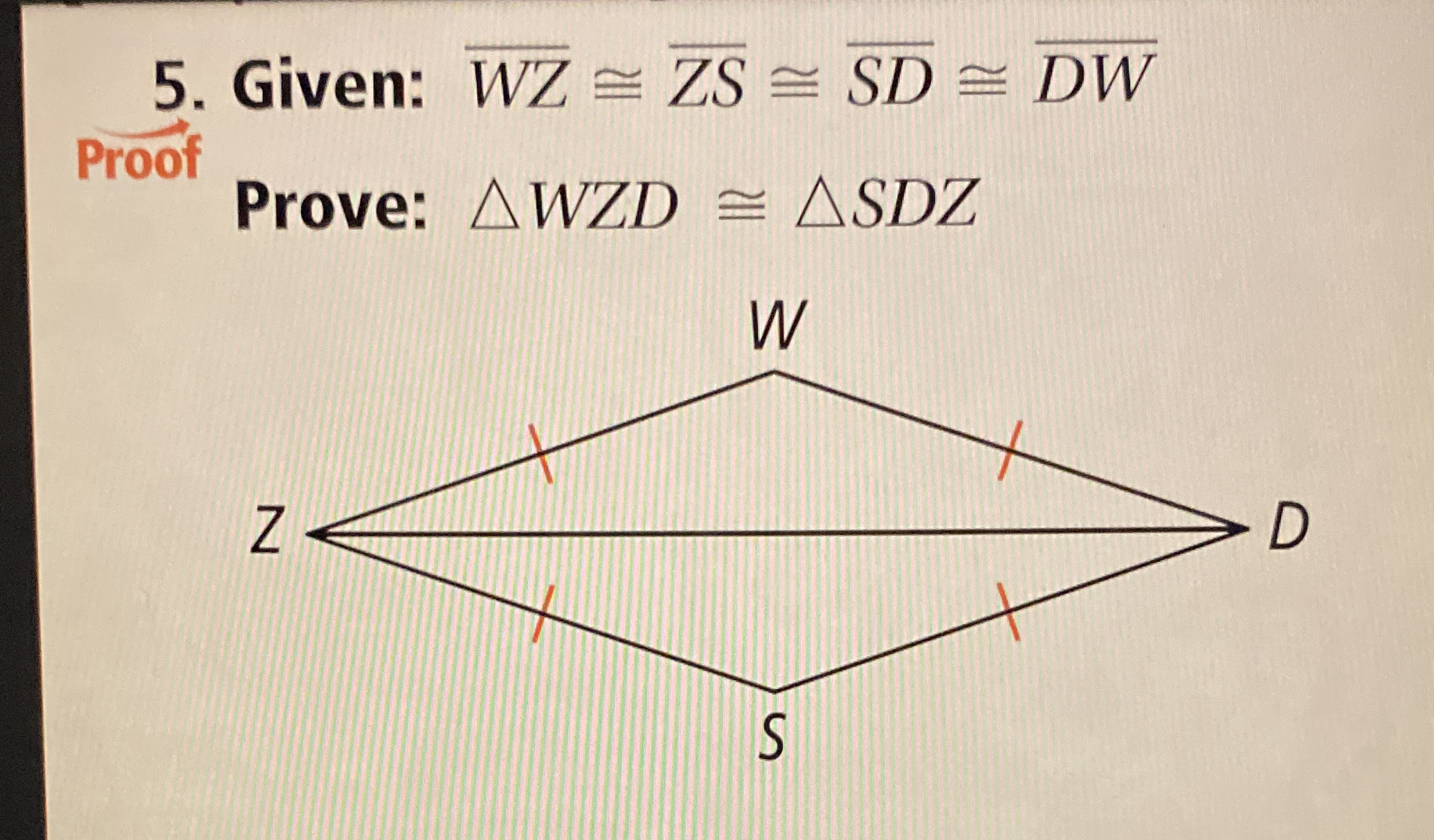
Given: WZ ≅ ZS ≅ SD ≅ DW; Prove: ∆WZD ≅ ∆SDZ.

Understand the Problem

The question is asking to prove that the triangles WZD and SDZ are congruent given certain equal line segments. The proof will involve applying geometric properties and congruence postulates.

Answer

$$\triangle WZD \cong \triangle SDZ$$

Steps to Solve

List the Given Information We are given that the segments are equal:

$WZ \cong ZS$
$SD \cong DW$

This indicates that the lengths of these segments are congruent.

Identify the Shared Side We see that both triangles share the side $Z$ (or $SZ$). This side is common to both triangles, which is an important aspect of congruent triangle proofs.
Use the Side-Side-Side (SSS) Postulate According to the SSS postulate, if three sides of one triangle are equal to three sides of another triangle, then the two triangles are congruent.

Since we have:

$WZ = ZS$
$SD = DW$
$ZW = ZD$ (common side)

We can say: $$\triangle WZD \cong \triangle SDZ$$

Conclude the Proof With the above statements established, we can conclude that the triangles are congruent by the SSS postulate.

$$\triangle WZD \cong \triangle SDZ$$

More Information

This proof demonstrates the congruence of the triangles based on equal side lengths. Congruent triangles have identical shapes and sizes, which means their corresponding parts are equal.

Tips

Not Identifying Shared Sides: Students might forget to recognize the shared side between the two triangles.
Misapplying Postulates: Ensure that the correct congruence postulate is applied; here, SSS is appropriate due to the equal sides.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!