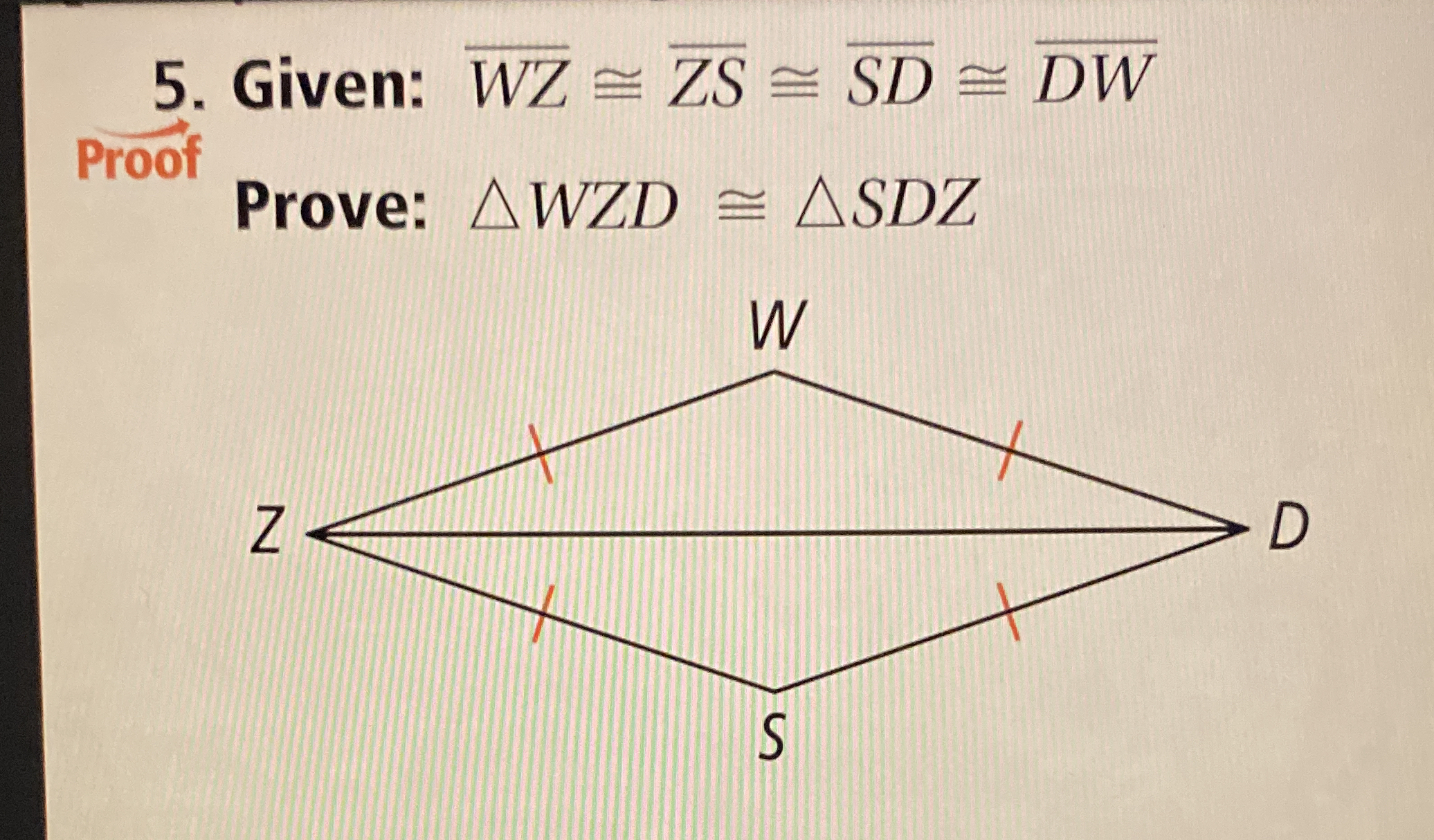
Given: WZ ≅ ZS ≅ SD ≅ DW. Prove: ΔWZD ≅ ΔSDZ.
Understand the Problem
The question involves proving the congruence of two triangles, ΔWZD and ΔSDZ, given that certain line segments are congruent. The focus is on applying geometric principles and properties to establish the congruence of the triangles based on the provided information.
Answer
$$ \triangle WZD \cong \triangle SDZ $$
Answer for screen readers
$$ \triangle WZD \cong \triangle SDZ $$
Steps to Solve
-
Identify Congruent Sides Given that $WZ \cong ZS \cong SD \cong DW$, we know the lengths of these segments are equal. Thus, we have:
- $WZ = a$
- $ZS = a$
- $SD = a$
- $DW = a$
-
Establish Corresponding Angles Since segments $WZ$ and $SD$ are equal and they are opposite to angles, we can infer that $\angle WZD \cong \angle SDZ$. This can be observed due to the properties of isosceles triangles formed by the equal segments.
-
Apply the SAS Congruence Postulate Now, we can apply the SAS (Side-Angle-Side) postulate for triangle congruence:
- $WZ$ is side 1,
- $SD$ is side 2,
- $\angle WZD$ is the included angle.
Since two sides and the included angle of triangle $WZD$ are congruent to two sides and the included angle of triangle $SDZ$, we can conclude: $$ \triangle WZD \cong \triangle SDZ $$
$$ \triangle WZD \cong \triangle SDZ $$
More Information
The proof shows that congruent sides with an included angle prove the two triangles are congruent by the SAS postulate. This illustrates an important concept in triangle congruence.
Tips
- Misidentifying Angles: A common error is to assume angles are congruent without proper justification. Always ensure you have an explanation for angle congruence.
- Confusing Triangle Properties: Be careful when applying congruence postulates to ensure you’re referencing the correct triangles and sides.
AI-generated content may contain errors. Please verify critical information