Given W and Y are two events of an experiment with P(W) = 0.33, P(Y) = 0.42, and P(W U Y) = 0.67, calculate the following probabilities: (a) P(Y complement) = ? (b) P(W complement... Given W and Y are two events of an experiment with P(W) = 0.33, P(Y) = 0.42, and P(W U Y) = 0.67, calculate the following probabilities: (a) P(Y complement) = ? (b) P(W complement intersect Y complement) = ? (c) P(W complement union Y complement) = ?
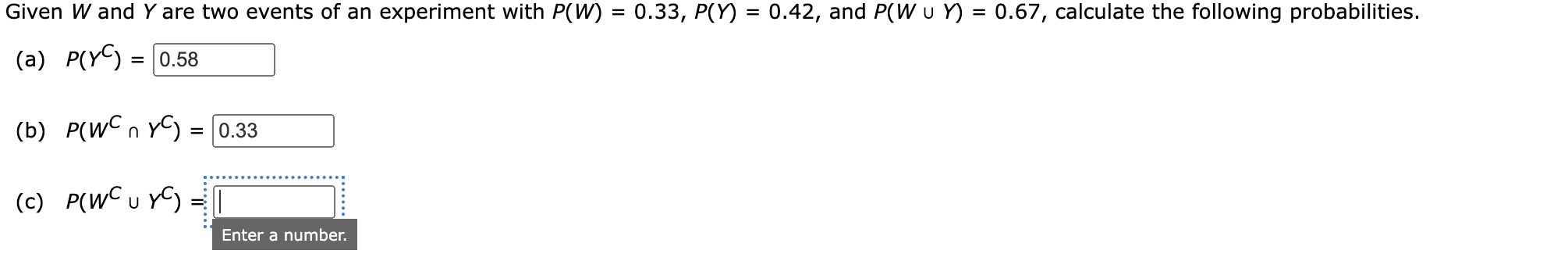
Understand the Problem
The question provides probabilities for events W and Y, specifically P(W), P(Y), and P(W union Y). The question asks to calculate the following probabilities: P(Y complement), P(W complement intersect Y complement) and P(W complement union Y complement).
Answer
(a) $P(Y^C) = 0.58$ (b) $P(W^C \cap Y^C) = 0.33$ (c) $P(W^C \cup Y^C) = 0.92$
Answer for screen readers
(a) $P(Y^C) = 0.58$ (b) $P(W^C \cap Y^C) = 0.33$ (c) $P(W^C \cup Y^C) = 0.92$
Steps to Solve
-
Calculate $P(Y^C)$ The probability of the complement of an event Y is given by $P(Y^C) = 1 - P(Y)$. We are given $P(Y) = 0.42$, so $P(Y^C) = 1 - 0.42 = 0.58$.
-
Calculate $P(W^C \cap Y^C)$ Using De Morgan's Law, we have $P(W^C \cap Y^C) = P((W \cup Y)^C)$. Therefore, $P(W^C \cap Y^C) = 1 - P(W \cup Y)$. We are given $P(W \cup Y) = 0.67$, so $P(W^C \cap Y^C) = 1 - 0.67 = 0.33$.
-
Calculate $P(W^C \cup Y^C)$ Using De Morgan's Law, we have $P(W^C \cup Y^C) = P((W \cap Y)^C) = 1 - P(W \cap Y)$. We know that $P(W \cup Y) = P(W) + P(Y) - P(W \cap Y)$. So, $P(W \cap Y) = P(W) + P(Y) - P(W \cup Y) = 0.33 + 0.42 - 0.67 = 0.08$. Therefore, $P(W^C \cup Y^C) = 1 - P(W \cap Y) = 1 - 0.08 = 0.92$.
(a) $P(Y^C) = 0.58$ (b) $P(W^C \cap Y^C) = 0.33$ (c) $P(W^C \cup Y^C) = 0.92$
More Information
The complement of a set contains everything that is not in the original set. De Morgan's Laws provide a relationship between unions, intersections, and complements.
Tips
A common mistake is to confuse the union and intersection symbols, which would lead to incorrectly calculating $P(W \cap Y)$ and subsequent probabilities. Another common mistake is misremembering or misapplying De Morgan's Laws when dealing with complements of unions or intersections.
AI-generated content may contain errors. Please verify critical information