Given the graph of f(x), evaluate the following expressions involving f(x). a. lim (x->-1) f(x) b. lim (x->-2) f(x) c. lim (x->2+) f(x) d. lim (x->2-) f(x) e. f(-2) f. lim (x->2) f... Given the graph of f(x), evaluate the following expressions involving f(x). a. lim (x->-1) f(x) b. lim (x->-2) f(x) c. lim (x->2+) f(x) d. lim (x->2-) f(x) e. f(-2) f. lim (x->2) f(x) g. lim (x->-2+) f(x) h. lim (x->2) f(x) this is a duplicate to part f i. f(2)
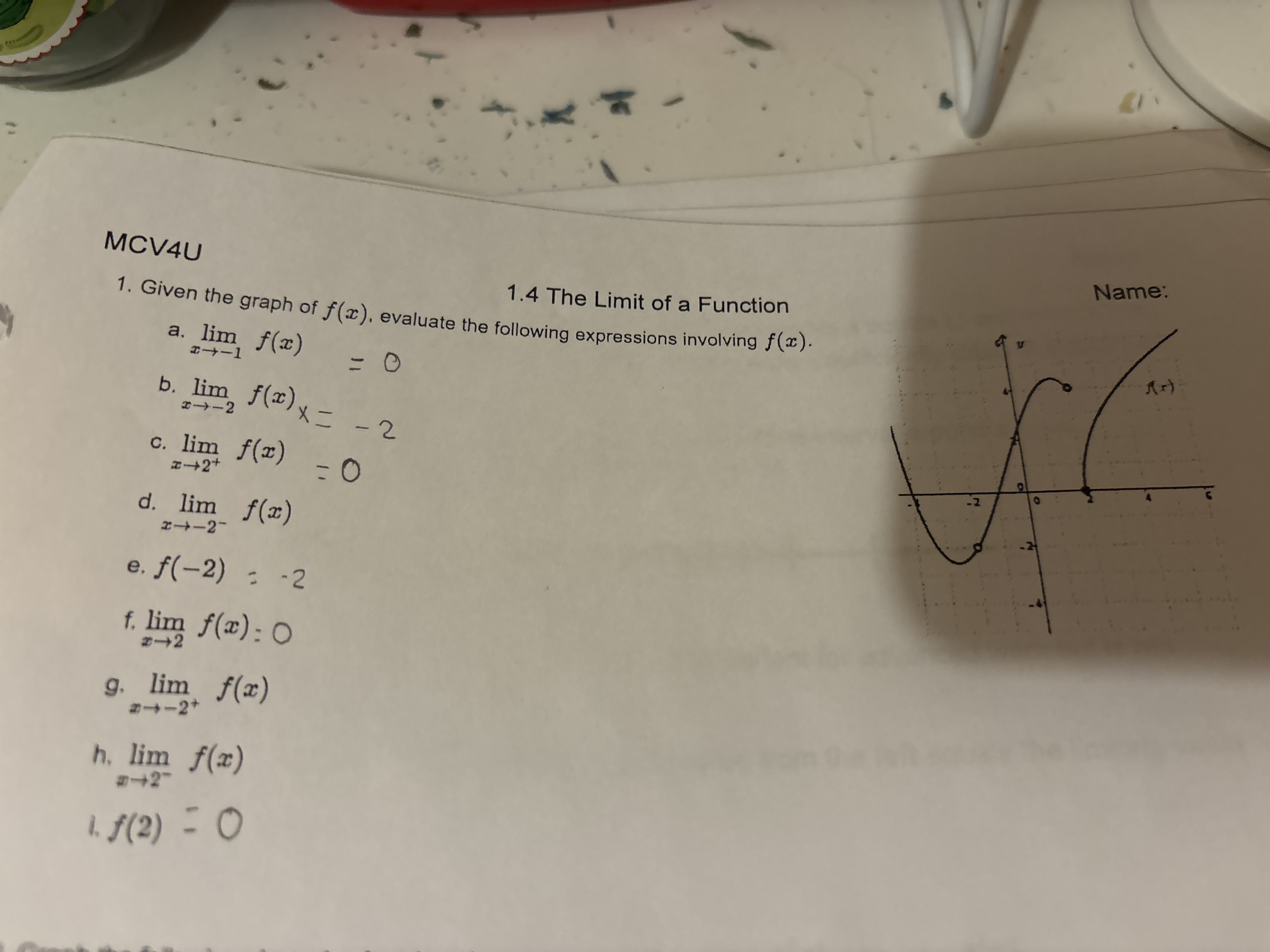
Understand the Problem
The question provides a graph of a function f(x) and asks us to evaluate several expressions involving limits and function values at specific points. We need to analyze the graph to determine the left-hand limit, right-hand limit, and function value at given x-values.
Answer
a. 0 b. Does not exist c. 2 d. 0 e. -2 f. Does not exist g. 4 h. Does not exist i. 0
Answer for screen readers
a. $\lim_{x \to -1} f(x) = 0$ b. $\lim_{x \to -2} f(x)$ does not exist. c. $\lim_{x \to 2^{+}} f(x) = 2$ d. $\lim_{x \to 2^{-}} f(x) = 0$ e. $f(-2) = -2$ f. $\lim_{x \to 2} f(x)$ does not exist. g. $\lim_{x \to -2^{+}} f(x) = 4$ h. $\lim_{x \to 2} f(x)$ does not exist. i. $f(2) = 0$
Steps to Solve
- Evaluate $\lim_{x \to -1} f(x)$
As $x$ approaches $-1$ from both sides, the function $f(x)$ approaches $0$.
$\lim_{x \to -1} f(x) = 0$
- Evaluate $\lim_{x \to -2} f(x)$
As $x$ approaches $-2$ from the left side ($x \to -2^{-}$), $f(x)$ approaches $-2$. As $x$ approaches $-2$ from the right side ($x \to -2^{+}$), $f(x)$ approaches $4$. Since the left-hand limit and right-hand limit are not equal, the limit does not exist.
Thus, $\lim_{x \to -2} f(x)$ does not exist.
- Evaluate $\lim_{x \to 2^{+}} f(x)$
As $x$ approaches $2$ from the right side, the function $f(x)$ approaches $2$.
$\lim_{x \to 2^{+}} f(x) = 2$
- Evaluate $\lim_{x \to 2^{-}} f(x)$
As $x$ approaches $2$ from the left side, the function $f(x)$ approaches $0$.
$\lim_{x \to 2^{-}} f(x) = 0$
- Evaluate $f(-2)$
The function value at $x=-2$ is $-2$.
$f(-2) = -2$
- Evaluate $\lim_{x \to 2} f(x)$
Since the left-hand limit $\lim_{x \to 2^{-}} f(x) = 0$ and the right-hand limit $\lim_{x \to 2^{+}} f(x) = 2$ are not equal, the $\lim_{x \to 2} f(x)$ does not exist.
- Evaluate $\lim_{x \to -2^{+}} f(x)$
As $x$ approaches $-2$ from the right side, $f(x)$ approaches $4$.
$\lim_{x \to -2^{+}} f(x) = 4$
- Evaluate $\lim_{x \to 2} f(x)$
As determined in step 6, since the left-hand limit and right-hand limit are not equal, the $\lim_{x \to 2} f(x)$ does not exist.
- Evaluate $f(2)$
The function value at $x=2$ is $0$.
$f(2) = 0$
a. $\lim_{x \to -1} f(x) = 0$ b. $\lim_{x \to -2} f(x)$ does not exist. c. $\lim_{x \to 2^{+}} f(x) = 2$ d. $\lim_{x \to 2^{-}} f(x) = 0$ e. $f(-2) = -2$ f. $\lim_{x \to 2} f(x)$ does not exist. g. $\lim_{x \to -2^{+}} f(x) = 4$ h. $\lim_{x \to 2} f(x)$ does not exist. i. $f(2) = 0$
More Information
Limits describe the value that a function approaches as the input (or independent variable) approaches some value. A one-sided limit considers the values of $x$ approaching from only one direction (either from the left or right). The function value at a point is simply the y-value of the function at the given x-value.
Tips
A common mistake is confusing the limit of a function as $x$ approaches a value 'a' with the value of the function at $x=a$. The limit describes the value the function is approaching, while the function value is the actual value of the function at that point. Also, students may incorrectly evaluate one-sided limits, by not approaching from the correct side.
AI-generated content may contain errors. Please verify critical information