Expand (5s+6)(s-2).
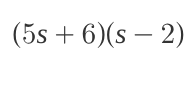
Understand the Problem
The question asks to expand the expression (5s+6)(s-2). This involves using the distributive property (often referred to as the FOIL method) to multiply each term in the first binomial by each term in the second binomial, and then combining like terms to simplify the result.
Answer
$5s^2 - 4s - 12$
Answer for screen readers
$5s^2 - 4s - 12$
Steps to Solve
-
Apply the distributive property (FOIL method) Multiply each term in the first binomial $(5s + 6)$ by each term in the second binomial $(s - 2)$. $$ (5s + 6)(s - 2) = 5s(s) + 5s(-2) + 6(s) + 6(-2) $$
-
Perform the multiplication Multiply each term out: $$ 5s(s) = 5s^2 $$ $$ 5s(-2) = -10s $$ $$ 6(s) = 6s $$ $$ 6(-2) = -12 $$ So the expression becomes: $$ 5s^2 - 10s + 6s - 12 $$
-
Combine like terms Combine the '$s$' terms: $-10s + 6s = -4s$.
-
Write the final expression The final expanded form is: $$ 5s^2 - 4s - 12 $$
$5s^2 - 4s - 12$
More Information
The expanded form of the given expression $(5s + 6)(s - 2)$ is $5s^2 - 4s - 12$.
Tips
A common mistake is not correctly applying the distributive property, especially with negative signs. Make sure to multiply each term in the first binomial by each term in the second binomial. Also, be careful when combining like terms, paying attention to the signs.
AI-generated content may contain errors. Please verify critical information