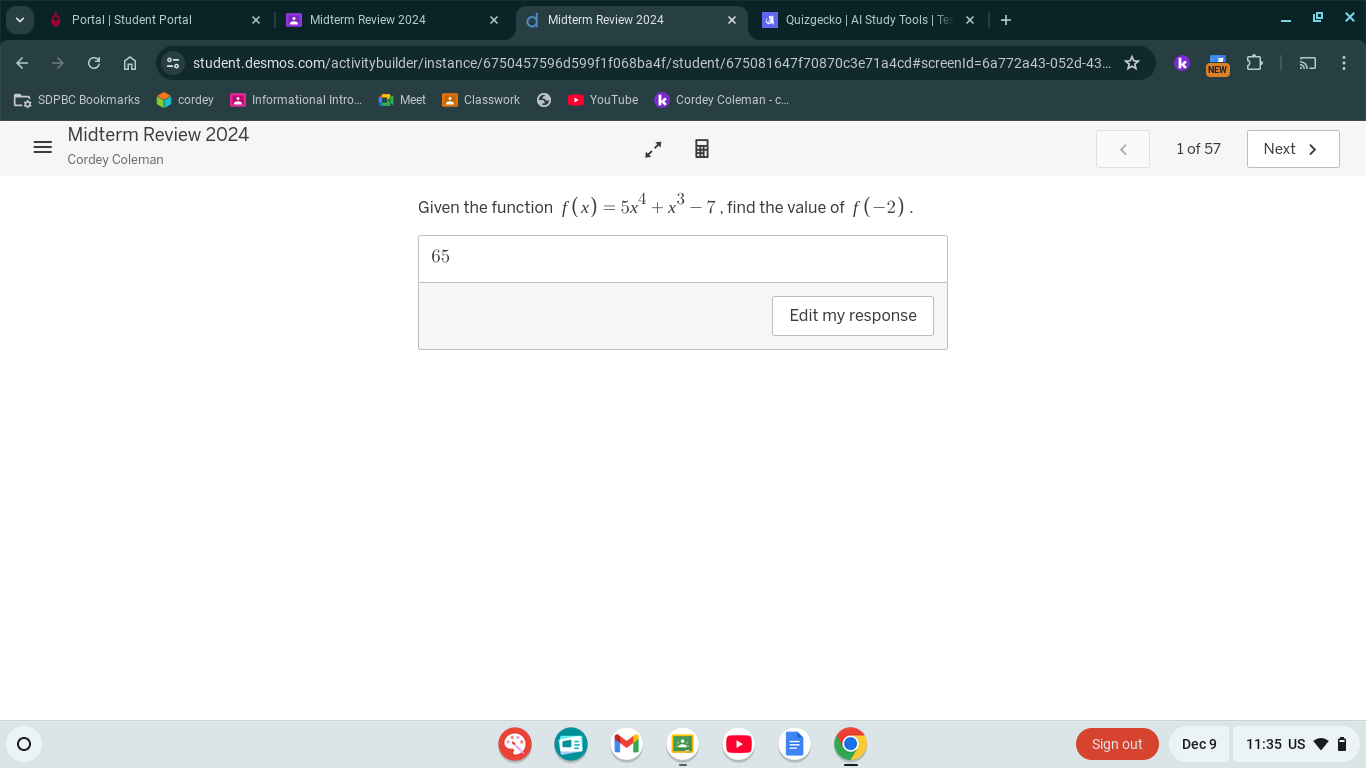
Given the function f(x) = 5x^4 + x^3 - 7, find the value of f(-2).
Understand the Problem
The question is asking us to evaluate the function f(x) = 5x^4 + x^3 - 7 at the point x = -2. This requires substituting -2 into the function and simplifying to find the corresponding output value.
Answer
The value of $f(-2)$ is $65$.
Answer for screen readers
The value of $f(-2)$ is $65$.
Steps to Solve
-
Substitute the value of x To find $f(-2)$, we substitute $-2$ into the function $f(x) = 5x^4 + x^3 - 7$.
This gives us: $$ f(-2) = 5(-2)^4 + (-2)^3 - 7 $$
-
Calculate $(-2)^4$ First we calculate $(-2)^4$: $$ (-2)^4 = 16 $$
-
Calculate $(-2)^3$ Next, calculate $(-2)^3$: $$ (-2)^3 = -8 $$
-
Plug values back into the function Now substitute these values back into the equation: $$ f(-2) = 5(16) + (-8) - 7 $$
-
Perform the multiplication Calculate the first term: $$ 5(16) = 80 $$
-
Combine all terms Now add the other terms: $$ f(-2) = 80 - 8 - 7 $$
-
Final calculation Compute the final result: $$ 80 - 8 = 72 $$ Then, $$ 72 - 7 = 65 $$
The value of $f(-2)$ is $65$.
More Information
The function evaluates polynomial expressions, and substituting values into the polynomial allows us to calculate specific outputs. Such calculations are common in algebra and can show how quickly polynomial values can change with different inputs.
Tips
- Confusing the power of negative numbers; remember to keep track of the signs correctly when raising negative numbers to even or odd powers.
- Forgetting to perform all arithmetic steps sequentially can lead to incorrect answers; ensure to combine all terms carefully.
AI-generated content may contain errors. Please verify critical information