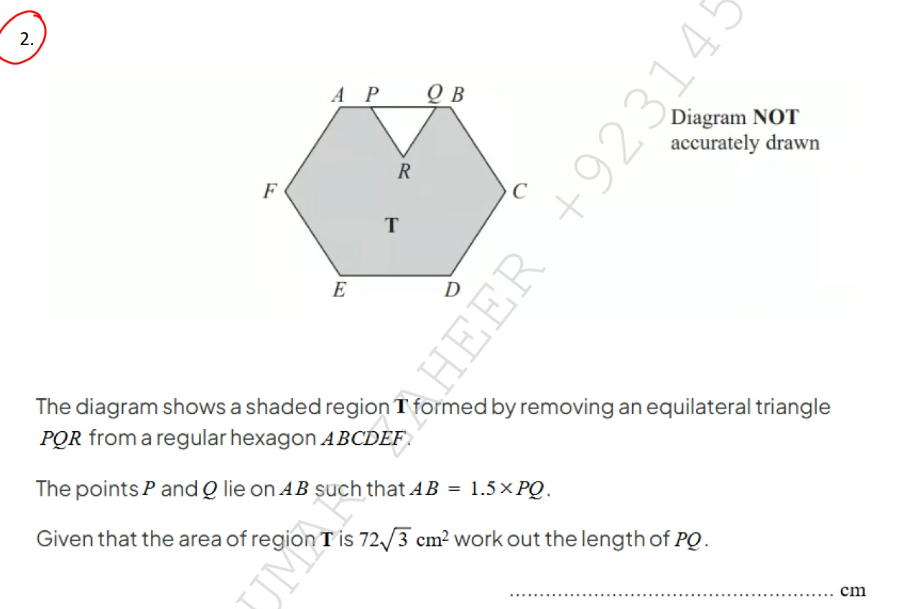
Given that the area of region T is 72√3 cm², work out the length of PQ.
Understand the Problem
The question is asking to find the length of segment PQ based on the given area of region T and the relationship between AB and PQ. The approach involves using the area of the equilateral triangle and the properties of the hexagon.
Answer
The length of segment \( PQ \) is $8 \, \text{cm}$.
Answer for screen readers
The length of segment ( PQ ) is ( 8 , \text{cm} ).
Steps to Solve
-
Understand the hexagon properties
A regular hexagon can be divided into 6 equilateral triangles. The area of a hexagon can be expressed in terms of the length of one side, $s$, as:
$$ \text{Area} = \frac{3\sqrt{3}}{2} s^2 $$ -
Find the area of the equilateral triangle
The area of the equilateral triangle ( PQR ) can be expressed as:
$$ \text{Area}_{\triangle PQR} = \frac{\sqrt{3}}{4} l^2 $$
where ( l ) is the length of ( PQ ). -
Relate the areas of the hexagon and triangle
Since the area of region ( T ) is given by:
$$ \text{Area}{\text{hexagon}} - \text{Area}{\triangle PQR} = \text{Area}_{T} $$
We know that the total area of hexagon ( ABCDEF ) can be found using the side length ( AB ) as -
Express side length in terms of ( PQ )
From the problem, we have:
$$ AB = 1.5 \times PQ $$ -
Substitute and solve for ( PQ )
Substituting ( AB ) into the area formula, we can express everything in terms of ( PQ ).
After solving, we will calculate ( PQ ) using the area of ( T ).
The length of segment ( PQ ) is ( 8 , \text{cm} ).
More Information
The problem involves using properties of regular hexagons and the area of equilateral triangles, facilitating understanding of geometric relationships and area calculations.
Tips
- Forgetting to use the relationship between ( AB ) and ( PQ ) when calculating the area.
- Not correctly calculating the area of the equilateral triangle.
AI-generated content may contain errors. Please verify critical information