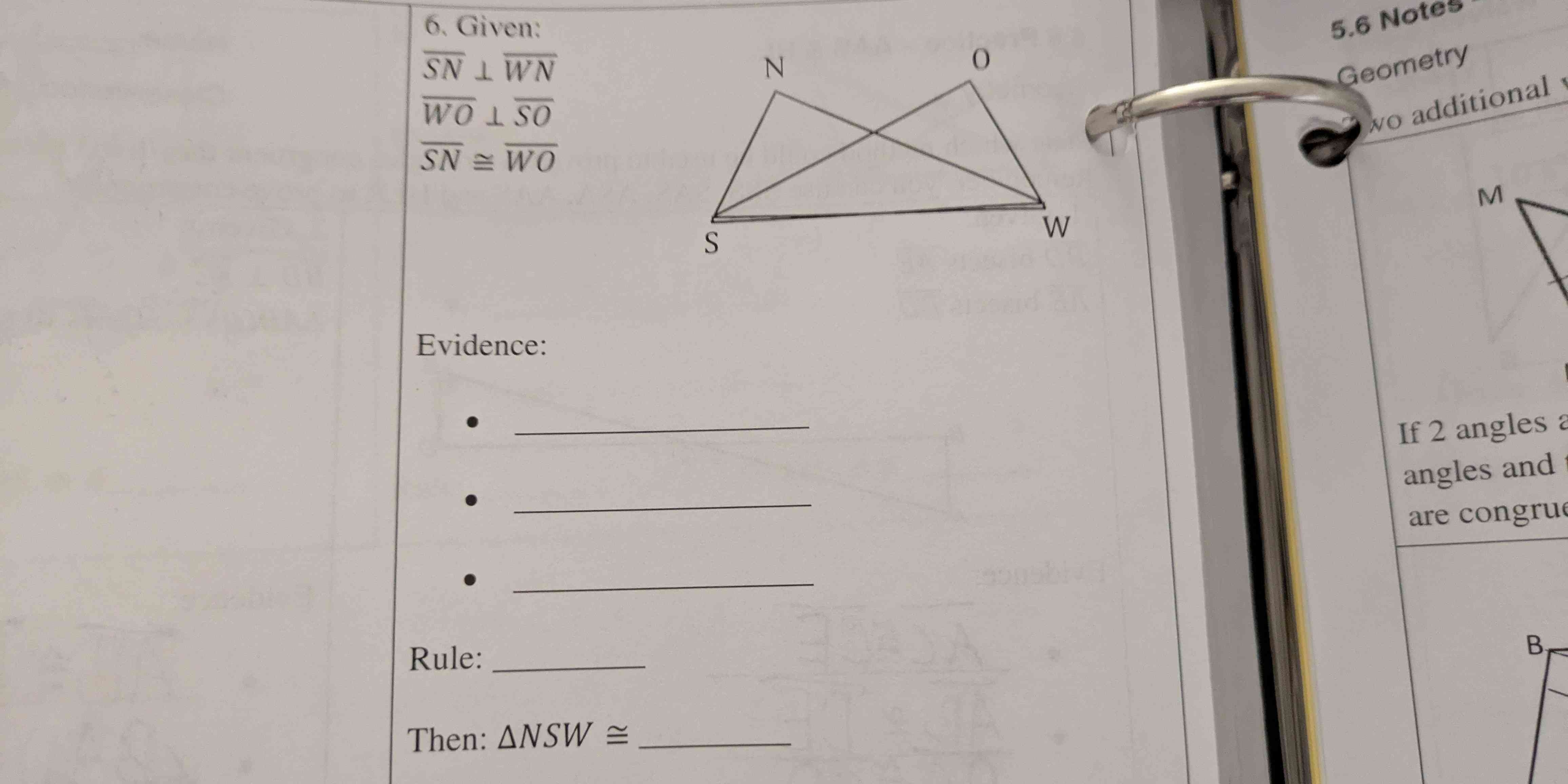
Given: SN ⊥ WN, WO ⊥ SO, SN ≅ WO. Evidence: • • • Rule: Then: ΔNSW ≅ _____
Understand the Problem
The question involves using given geometric properties to determine congruency between triangles. Specifically, it relates to triangle congruence based on provided angles and sides.
Answer
$$ \triangle NSW \cong \triangle OWS $$
Answer for screen readers
$$ \triangle NSW \cong \triangle OWS $$
Steps to Solve
- Identify the Given Information
The problem states the following:
- Line segment $SN$ is perpendicular to line segment $WN$ ($SN \perp WN$).
- Line segment $WO$ is perpendicular to line segment $SO$ ($WO \perp SO$).
- Line segment $SN$ is congruent to line segment $WO$ ($SN \cong WO$).
- Draw the Triangles
From the information provided, we can identify two triangles that are likely involved:
- Triangle $NSW$ composed of points $N$, $S$, and $W$.
- Triangle $OWS$ composed of points $O$, $W$, and $S$.
- Apply the Right Triangle Congruence Criteria
To prove the congruence of triangles, we will use the Right Angle Hypotenuse Leg (RHL) criterion:
If a right triangle has one leg congruent to the leg of another right triangle and the hypotenuse congruent as well, then the triangles are congruent.
From the information:
- Triangle $NSW$ has $SN \cong WO$ for legs.
- Both triangles have right angles formed by $SN$ and $WN$, as well as $WO$ and $SO$.
- Conclude Triangle Congruence
We can conclude:
$$ \triangle NSW \cong \triangle OWS $$
by the criteria of RHL (Right Angle, Hypotenuse, Leg).
$$ \triangle NSW \cong \triangle OWS $$
More Information
The congruence of triangles is important in geometry as it allows us to deduce properties and relationships based on angles and sides. In this case, right triangles with the same lengths and shared angles establish the congruence.
Tips
- Ignoring Right Angles: Make sure to account for right angles when determining if triangles are right triangles.
- Misidentifying Congruent Sides: Ensure that the sides you identify as congruent match the given information.
AI-generated content may contain errors. Please verify critical information