Given a right triangle with A = 100 and B = 64, work out C.
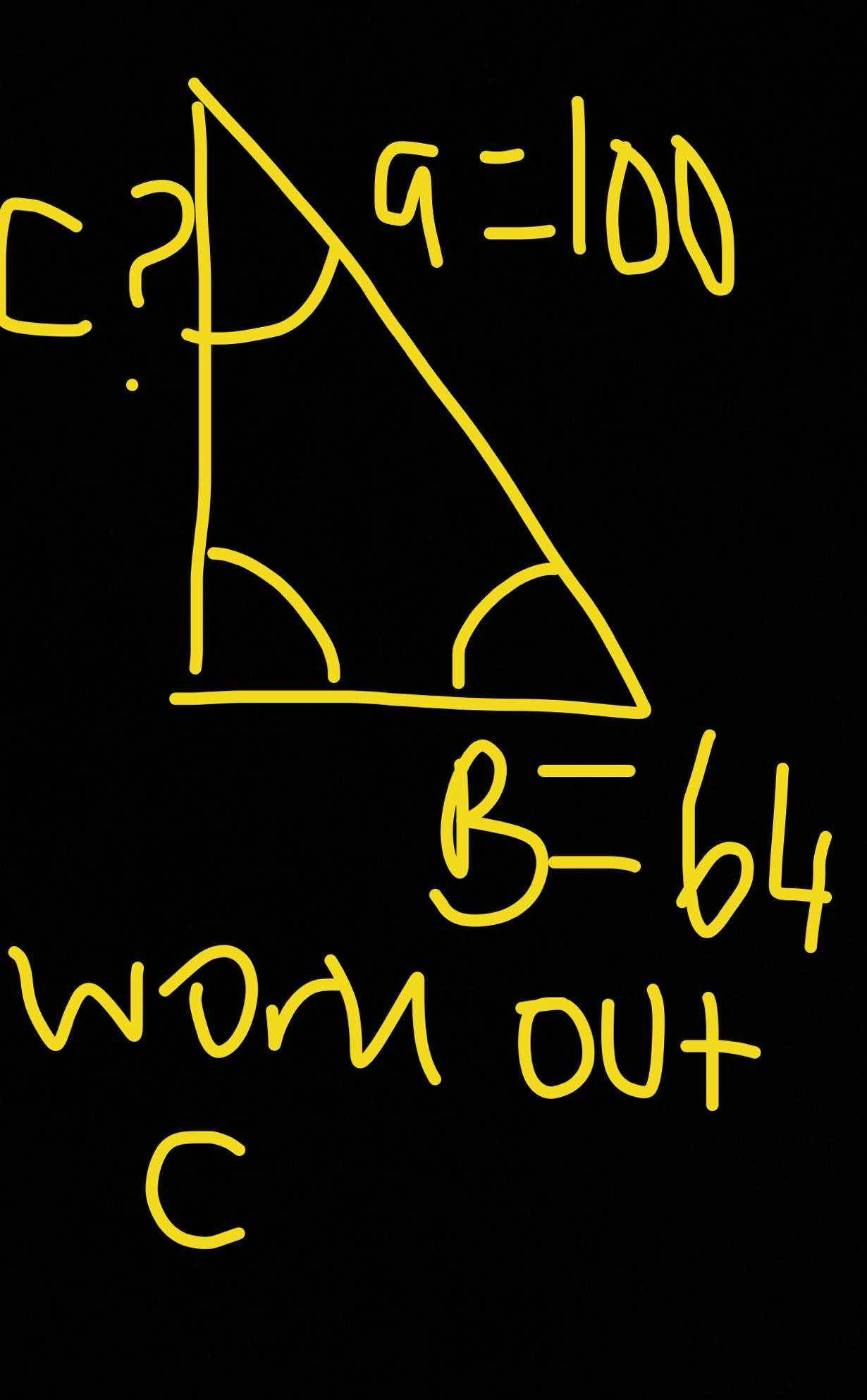
Understand the Problem
The question is asking to find the length of side C in a right triangle given that side A is 100 and side B is 64.
Answer
The length of side \( C \) is approximately \( 118.74 \).
Answer for screen readers
The length of side ( C ) is approximately ( 118.74 ).
Steps to Solve
-
Identify the formula for a right triangle In a right triangle, the Pythagorean Theorem relates the lengths of the sides. The theorem states that: $$ a^2 + b^2 = c^2 $$ where ( c ) is the length of the hypotenuse (side C), and ( a ) and ( b ) are the lengths of the other two sides (side A and side B).
-
Substitute the known values Given that ( a = 100 ) and ( b = 64 ), substitute these values into the equation: $$ 100^2 + 64^2 = c^2 $$
-
Calculate the squares of the sides Calculate ( 100^2 ) and ( 64^2 ): $$ 100^2 = 10000 $$ $$ 64^2 = 4096 $$
-
Add the squared values Now add the two results together: $$ 10000 + 4096 = c^2 $$ This gives: $$ 14096 = c^2 $$
-
Solve for ( c ) Take the square root of both sides to find ( c ): $$ c = \sqrt{14096} $$
-
Calculate the final value Using a calculator, find the square root: $$ c \approx 118.74 $$
The length of side ( C ) is approximately ( 118.74 ).
More Information
The Pythagorean Theorem is a fundamental principle in geometry, especially useful in calculating distances in right-angled triangles. The calculation process involving squaring the lengths, adding them, and then taking the square root is vital in many fields such as architecture and engineering.
Tips
- Forgetting to square the lengths before adding them.
- Confusing the sides ( A ), ( B ), and ( C )—remember that ( C ) is always the hypotenuse.
AI-generated content may contain errors. Please verify critical information