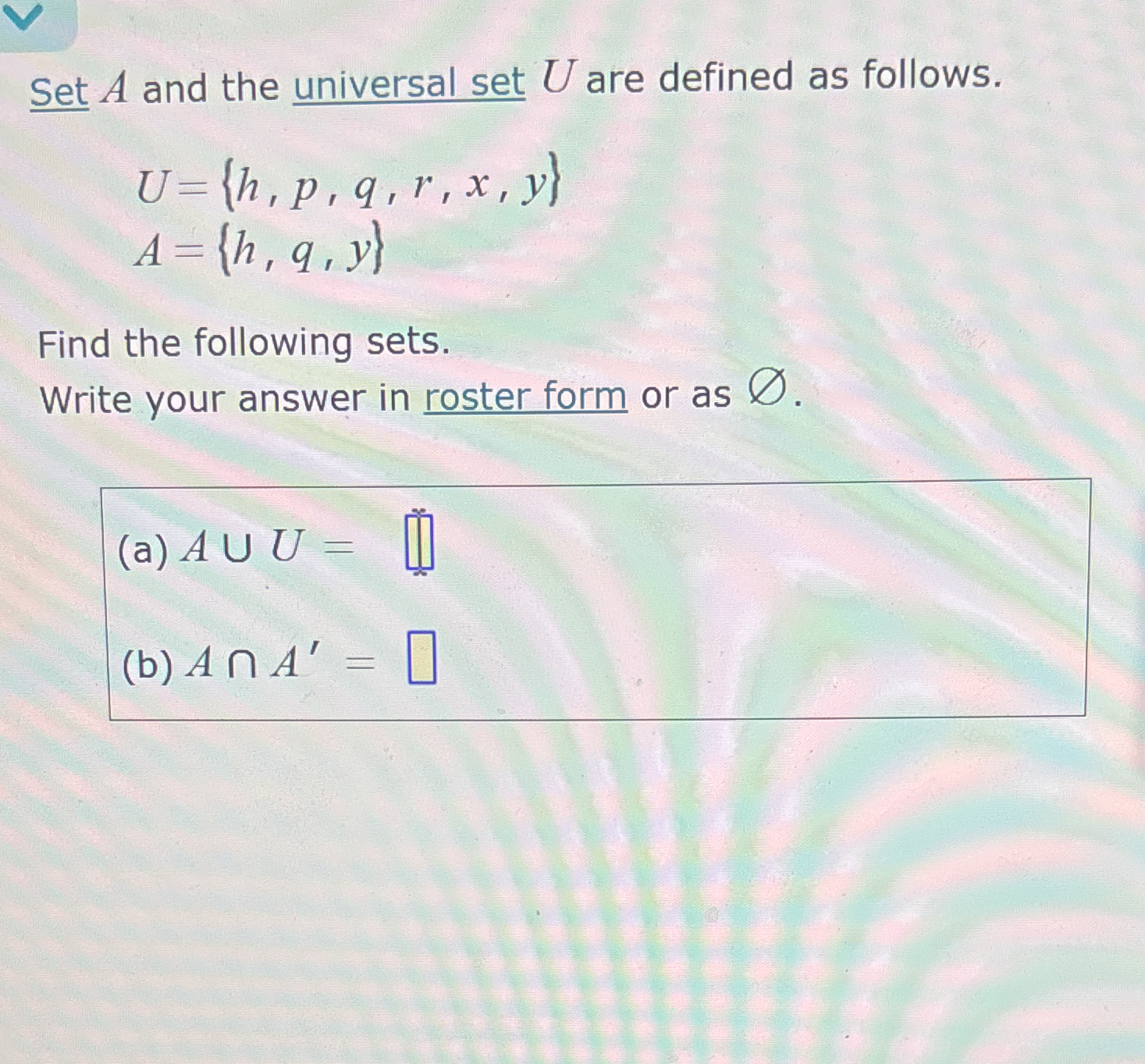
Given A = {h,q,y} and U = {h,p,q,r,x,y}, find: (a) A ∪ U = ? (b) A ∩ A' = ?
Understand the Problem
The question provides the elements of set A and the universal set U. Part (a) asks for the union of set A and set U. Part (b) asks for the intersection of set A and complement of set A (A'). The final answer must be in roster form or as the empty set symbol.
Answer
(a) $A \cup U = \{h, p, q, r, x, y\}$ (b) $A \cap A' = \emptyset$
Answer for screen readers
(a) $A \cup U = {h, p, q, r, x, y}$ (b) $A \cap A' = \emptyset$
Steps to Solve
- Find the union of A and U
The union of two sets, $A \cup U$, is the set of all elements that are in A, in U, or in both.
$A = {h, q, y}$ $U = {h, p, q, r, x, y}$
$A \cup U = {h, p, q, r, x, y}$
- Find the complement of A
The complement of set A, denoted as A', consists of all elements in the universal set U that are not in A.
$U = {h, p, q, r, x, y}$ $A = {h, q, y}$
$A' = {p, r, x}$
- Find the intersection of A and A'
The intersection of two sets, $A \cap A'$, is the set of all elements that are common to both A and A'.
$A = {h, q, y}$ $A' = {p, r, x}$
Since A and A' have no elements in common, their intersection is the empty set, denoted as $\emptyset$.
$A \cap A' = \emptyset$
(a) $A \cup U = {h, p, q, r, x, y}$ (b) $A \cap A' = \emptyset$
More Information
The union of any set and the universal set is always the universal set itself. The intersection of any set and its complement is always the empty set.
Tips
Null.
AI-generated content may contain errors. Please verify critical information