Calculate the current using KVL (Kirchhoff's Voltage Law) and KCL (Kirchhoff's Current Law).
Understand the Problem
The question asks to calculate the current in a circuit, by applying KVL (Kirchhoff's Voltage Law) and KCL (Kirchhoff's Current Law). We need to analyze the circuit diagram to determine the current values.
Answer
The current through the $7\ \Omega$ resistor is $-\frac{100}{91}\ A$.
Answer for screen readers
The current through the $7\ \Omega$ resistor is $-\frac{100}{91} \approx -1.099\ A$.
Steps to Solve
- Label the circuit
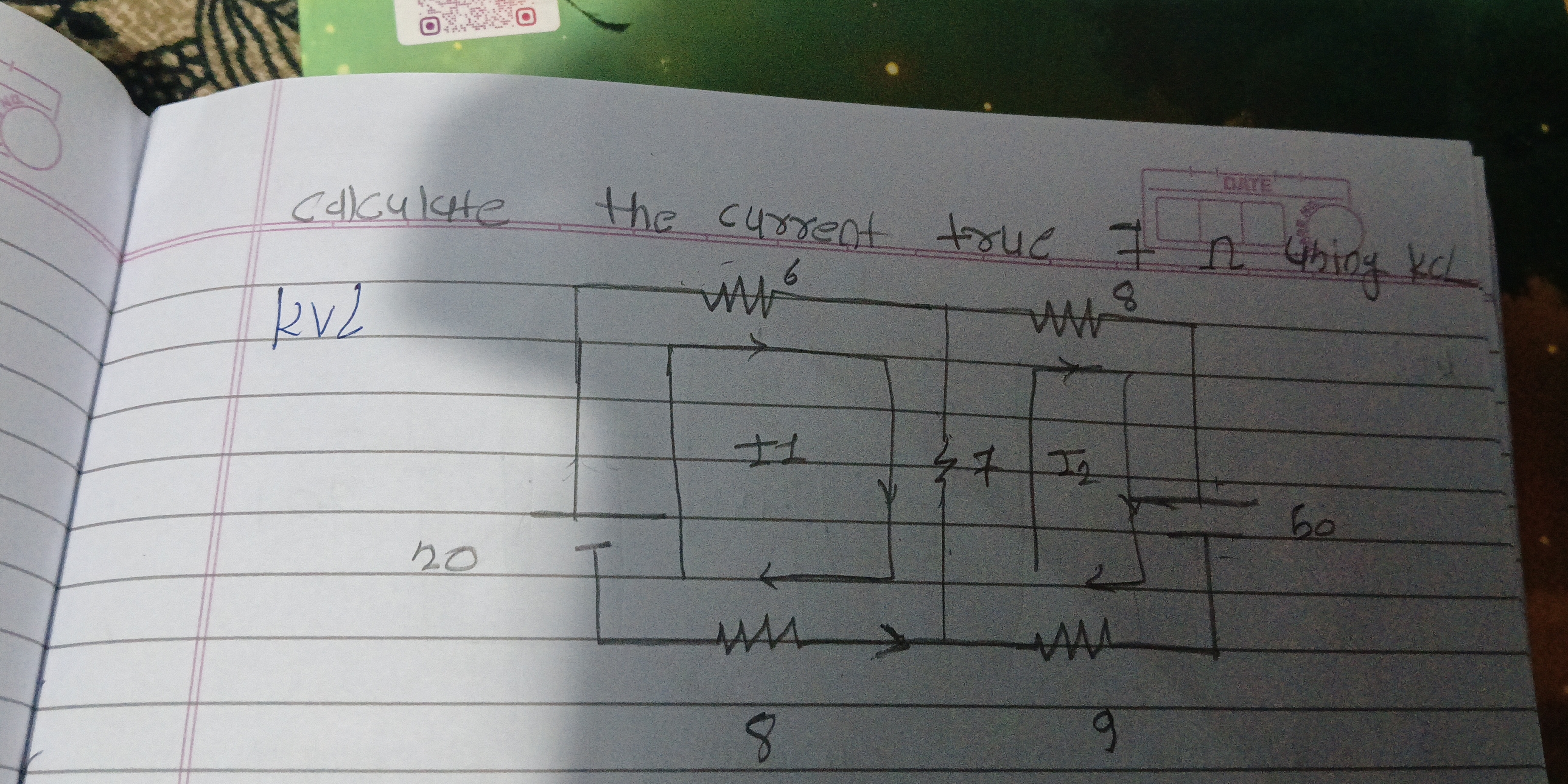
Label all the components of the circuit. Resistors are: $R_1 = 6\ \Omega$, $R_2 = 8\ \Omega$, $R_3 = 8\ \Omega$, $R_4 = 9\ \Omega$, and $R_5 = 7\ \Omega$. Voltage sources are: $V_1 = 20\ V$, $V_2 = 60\ V$. Also label loop currents $I_1$ and $I_2$ as indicated.
- Apply KVL to loop 1
Write the KVL equation for loop 1:
$20 - 6I_1 - 7(I_1 - I_2) - 8I_1 = 0$. Simplifying yields: $20 - 6I_1 - 7I_1 + 7I_2 - 8I_1 = 0$ $20 - 21I_1 + 7I_2 = 0$ $21I_1 - 7I_2 = 20$ (Equation 1)
- Apply KVL to loop 2
Write the KVL equation for loop 2:
$60 - 9I_2 - 7(I_2 - I_1) - 8I_2 = 0$ Simplifying yields: $60 - 9I_2 - 7I_2 + 7I_1 - 8I_2 = 0$ $60 - 24I_2 + 7I_1 = 0$ $7I_1 - 24I_2 = -60$ (Equation 2)
- Solve the simultaneous equations
We now have two equations: $21I_1 - 7I_2 = 20$ (Equation 1) $7I_1 - 24I_2 = -60$ (Equation 2)
Multiply Equation 2 by 3: $21I_1 - 72I_2 = -180$ (Equation 3)
Subtract Equation 3 from Equation 1: $(21I_1 - 7I_2) - (21I_1 - 72I_2) = 20 - (-180)$ $65I_2 = 200$ $I_2 = \frac{200}{65} = \frac{40}{13} \approx 3.077\ A$
Substitute $I_2$ into Equation 1: $21I_1 - 7 * \frac{40}{13} = 20$ $21I_1 = 20 + \frac{280}{13}$ $21I_1 = \frac{260 + 280}{13}$ $21I_1 = \frac{540}{13}$ $I_1 = \frac{540}{13 * 21} = \frac{540}{273} = \frac{180}{91} \approx 1.978\ A$
- Calculate the current through the $7 \Omega$ resistor
The current through the $7\ \Omega$ resistor is $I_1 - I_2$. $I_{7\Omega} = I_1 - I_2 = \frac{180}{91} - \frac{40}{13} = \frac{180}{91} - \frac{280}{91} = -\frac{100}{91} \approx -1.099\ A$
The current through the $7\ \Omega$ resistor is $-\frac{100}{91} \approx -1.099\ A$.
More Information
The negative sign indicates that the current's true direction is opposite to the originally assumed direction.
Tips
A common mistake is to incorrectly apply KVL or KCL, leading to errors in the equations governing the circuit. This can be avoided by carefully tracing each loop and node, ensuring that the signs are correct based on the assumed current directions and voltage polarities. Another mistake is in the algebraic manipulation while solving the simultaneous equations.
AI-generated content may contain errors. Please verify critical information