f(z) = γ²·cos²θ + i·γ²·sin²θ
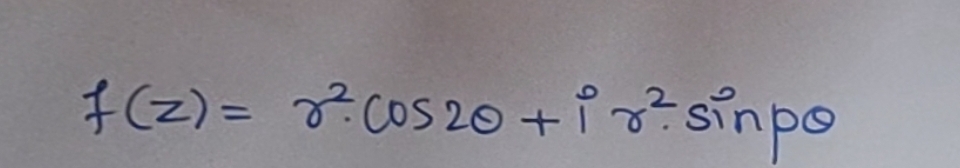
Understand the Problem
The question presents a function in the form of a complex equation involving trigonometric functions. The goal is likely to simplify or analyze this function in some way.
Answer
The simplified function is \( f(z) = \gamma^2 (\cos^2 \theta + i \sin^2 \theta) \).
Answer for screen readers
The simplified form of the function is: $$ f(z) = \gamma^2 (\cos^2 \theta + i \sin^2 \theta) $$
Steps to Solve
- Identify the function components
The function is given as ( f(z) = \gamma^2 \cos^2 \theta + i \gamma^2 \sin^2 \theta ). This involves a real part and an imaginary part.
- Separate real and imaginary parts
The real part of the function is ( \gamma^2 \cos^2 \theta ) and the imaginary part is ( i \gamma^2 \sin^2 \theta ).
- Factor out common terms
We can factor out ( \gamma^2 ) from both parts: $$ f(z) = \gamma^2 (\cos^2 \theta + i \sin^2 \theta) $$
- Use Euler's formula
Recall that ( e^{ix} = \cos x + i \sin x ). Using this, we rewrite the function: $$ f(z) = \gamma^2 \left(\cos^2 \theta + i \sin^2 \theta\right) $$
- Express in terms of ( \gamma^2 )
You can interpret this expression based on specific applications or values of ( \theta ).
The simplified form of the function is: $$ f(z) = \gamma^2 (\cos^2 \theta + i \sin^2 \theta) $$
More Information
This function represents a complex number influenced by the parameter ( \gamma ) and the angle ( \theta ). The function’s real part is related to the cosine squared function, while the imaginary part involves the sine squared function. This can be relevant in applications such as wave functions and signal processing.
Tips
- Ignoring the imaginary unit: Sometimes, it's easy to forget the factor of ( i ) when combining terms.
- Not recognizing common factors: Failing to factor out ( \gamma^2 ) can lead to unnecessarily complicated expressions.
AI-generated content may contain errors. Please verify critical information