\frac{\csc x}{5} - 2 = 0
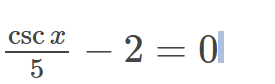
Understand the Problem
The question is asking to solve the equation involving the cosecant function. The goal is to isolate csc(x) and find the values of x that satisfy the equation.
Answer
$$ x \approx 0.1001674 + 2k\pi \quad \text{and} \quad x \approx 3.0414252 + 2k\pi $$
Answer for screen readers
The solutions are:
$$ x \approx 0.1001674 + 2k\pi \quad \text{and} \quad x \approx 3.0414252 + 2k\pi, \quad k \in \mathbb{Z} $$
Steps to Solve
- Isolate the cosecant function
Start by moving the constant term to the other side of the equation.
$$ \frac{\csc x}{5} = 2 $$
- Multiply by 5
To get rid of the fraction, multiply both sides of the equation by 5.
$$ \csc x = 10 $$
- Convert to sine function
Recall that the cosecant function is the reciprocal of the sine function. Thus, we can rewrite the equation as:
$$ \sin x = \frac{1}{10} $$
- Find the general solution
The sine function has a range of values between -1 and 1. Since $\sin x = \frac{1}{10}$, the general solutions can be expressed as:
$$ x = \arcsin\left(\frac{1}{10}\right) + 2k\pi \quad \text{and} \quad x = \pi - \arcsin\left(\frac{1}{10}\right) + 2k\pi \quad \text{for} ; k \in \mathbb{Z} $$
- Calculate the specific angle
Using a calculator, we find:
$$ \arcsin\left(\frac{1}{10}\right) \approx 0.1001674 \text{ radians} $$
So,
$$ x \approx 0.1001674 + 2k\pi \quad \text{and} \quad x \approx \pi - 0.1001674 + 2k\pi $$
- Simplify the second solution
Calculate the second solution:
$$ \pi - 0.1001674 \approx 3.0414252 $$
Thus the two solutions become:
$$ x \approx 0.1001674 + 2k\pi \quad \text{and} \quad x \approx 3.0414252 + 2k\pi $$
The solutions are:
$$ x \approx 0.1001674 + 2k\pi \quad \text{and} \quad x \approx 3.0414252 + 2k\pi, \quad k \in \mathbb{Z} $$
More Information
The solutions represent angles where the sine function yields $\frac{1}{10}$. This equation reflects concepts of trigonometric functions and their inverses. The general solutions account for periodicity of the sine function.
Tips
- Ignoring the periodic nature: Failing to add the $2k\pi$ term can lead to missing solutions.
- Miscalculating arcsine: Always check that the calculator is in the correct mode (radians vs. degrees).
AI-generated content may contain errors. Please verify critical information