\( \frac{3ab^{5}}{3a^{8}b^{6}} \)
Understand the Problem
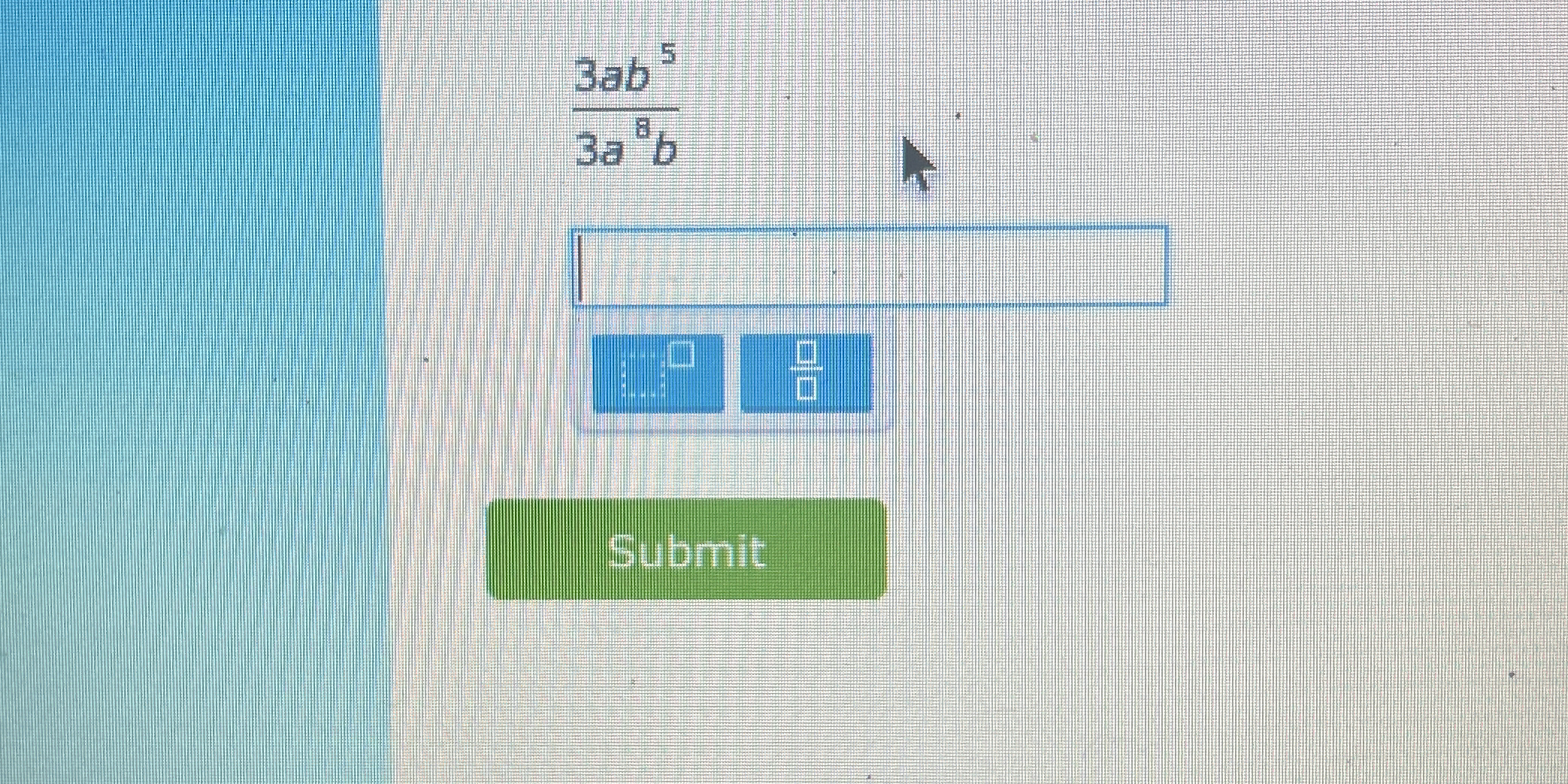
The question asks for the evaluation or simplification of the algebraic expression given in the image, specifically the fraction with variables and exponents. To solve it, we will apply algebraic rules to simplify the expression.
Answer
The simplified expression is \( \frac{1}{a^{7}b} \).
Answer for screen readers
The simplified expression is ( \frac{1}{a^{7}b} ).
Steps to Solve
-
Identify the Expression The given expression is ( \frac{3ab^{5}}{3a^{8}b^{6}} ).
-
Cancel Common Factors Notice that (3) in the numerator and the denominator can be simplified: $$ \frac{3}{3} = 1. $$ So, the expression simplifies to: $$ \frac{ab^{5}}{a^{8}b^{6}}. $$
-
Simplify the Variables Now, simplify the (a) terms: $$ \frac{a}{a^{8}} = a^{1-8} = a^{-7}. $$ Next, simplify the (b) terms: $$ \frac{b^{5}}{b^{6}} = b^{5-6} = b^{-1}. $$
-
Combine the Results Combining these results gives: $$ a^{-7}b^{-1}. $$
-
Express in Positive Exponents Using the property that (x^{-n} = \frac{1}{x^{n}}), rewrite the expression: $$ a^{-7}b^{-1} = \frac{1}{a^{7}b}. $$
The simplified expression is ( \frac{1}{a^{7}b} ).
More Information
This expression indicates that the output is dependent on the values of (a) and (b). If either variable is zero, the expression becomes undefined, which is an important consideration in algebra.
Tips
- Failing to cancel out the common factors properly in the fraction.
- Misapplying the properties of exponents, especially when reducing terms.
AI-generated content may contain errors. Please verify critical information