Form a quadratic equation whose roots are 3 - 7i and 3 - 2i.
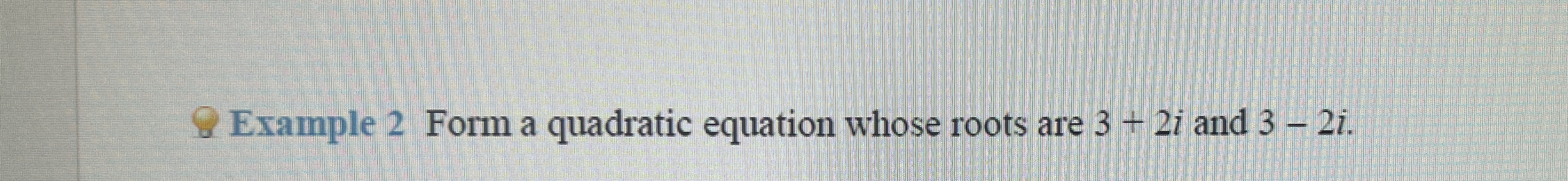
Understand the Problem
The question is asking to form a quadratic equation given the roots, which are specific complex numbers. This involves using the relationship between the roots and coefficients of a quadratic equation.
Answer
The quadratic equation is $x^2 - 6x + 10 = 0$.
Answer for screen readers
The quadratic equation is $x^2 - 6x + 10 = 0$.
Steps to Solve
-
Identify the Roots The roots given are (3 + i) and (3 - 2i).
-
Write the Factors The factors corresponding to these roots can be expressed as: $$(x - (3 + i))(x - (3 - 2i))$$
-
Expand the Factors Now, expand the product of the factors. First, write it out: $$(x - 3 - i)(x - 3 + 2i)$$
Now using the distributive property (FOIL):
- ( (x - 3)(x - 3) = x^2 - 6x + 9 )
- ( -i(x - 3) + 2i(x - 3) = (2i - i)(x - 3) = i(x - 3) )
Combining all: $$x^2 - 6x + 9 + i(2x - 6)$$
-
Combine Real and Imaginary Parts To find the final quadratic equation, since we want the polynomial with real coefficients, we can directly work with its simplified factorization:
-
Write: $$ (x - (3+i))(x - (3-2i)) $$
-
Group terms and simplify: $$ (x - 3 - i)(x - 3 + 2i) = ( (x - 3)^2 + 1^2 ) $$ Thus, the quadratic expands to: $$ (x - 3)^2 + 1 = (x^2 - 6x + 9 + 1) = x^2 - 6x + 10 $$.
-
Final Equation Thus, the quadratic equation whose roots are (3 + i) and (3 - 2i) is: $$x^2 - 6x + 10 = 0$$.
The quadratic equation is $x^2 - 6x + 10 = 0$.
More Information
This quadratic equation represents a polynomial with complex roots, illustrating that the coefficients remain real despite the complex roots.
Tips
- Mixing up the roots: Ensure you correctly identify and represent the complex numbers.
- Neglecting to set the equation to zero: Always remember to properly format the polynomial to equal zero for the standard form.
AI-generated content may contain errors. Please verify critical information