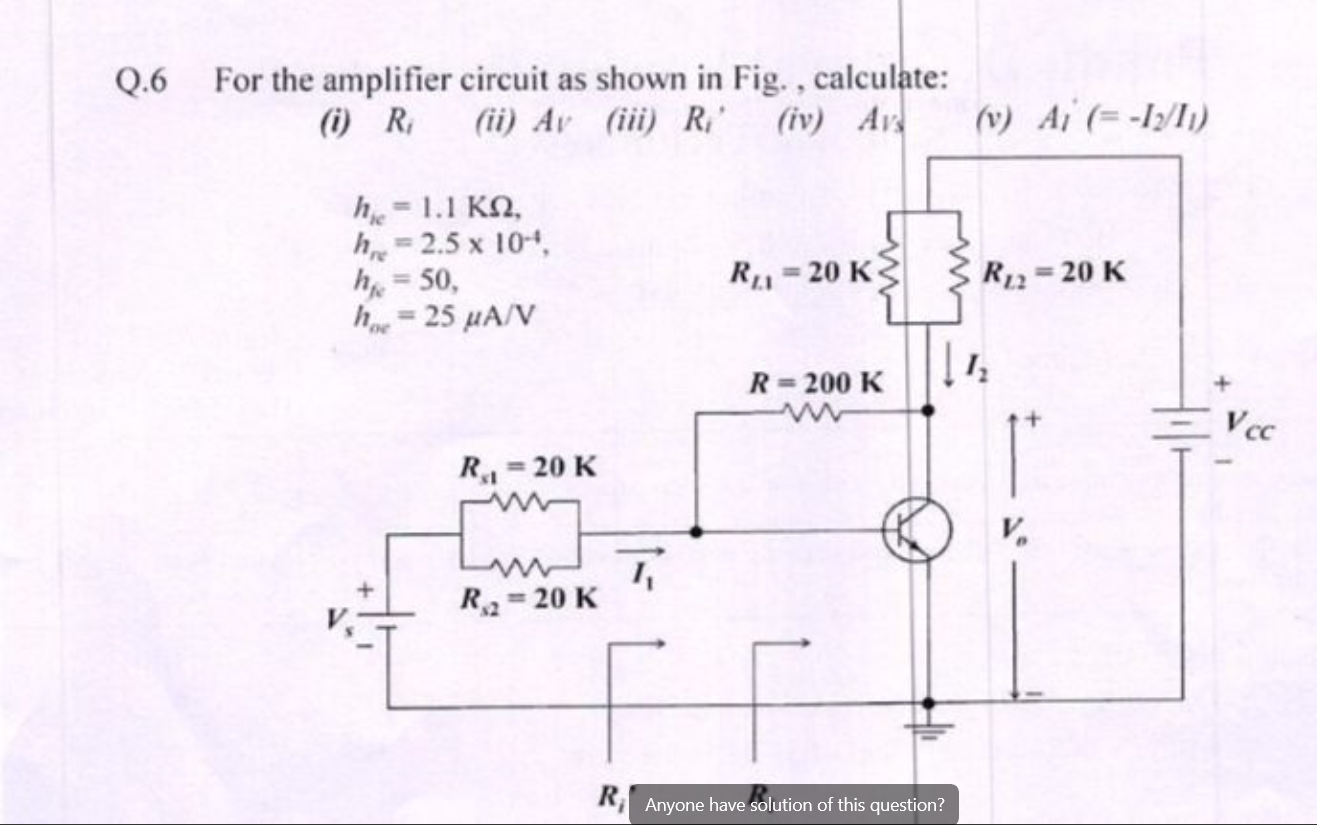
For the amplifier circuit as shown in Fig., calculate: (i) Ri (ii) Av (iii) Ri (iv) Avs (v) Ai (= -I2/I1)

Steps to Solve

1. Calculate Input Resistance ($R_i$)

The input resistance can be calculated using the formula: $$ R_i = R_{s1} \parallel R_{s2} $$

Where,

• $R_{s1} = 20 , k\Omega$
• $R_{s2} = 20 , k\Omega$

Using the formula for parallel resistances: $$ R_i = \frac{R_{s1} \cdot R_{s2}}{R_{s1} + R_{s2}} $$

Substituting the values: $$ R_i = \frac{20 \times 20}{20 + 20} = \frac{400}{40} = 10 , k\Omega $$

2. Calculate Voltage Gain ($A_v$)

The voltage gain can be calculated using the following formula: $$ A_v = -h_{fe} \cdot \left(\frac{R_{L1} \parallel R_{L2}}{R_{i}} \right) $$

Where,

• $h_{fe} = 50$
• $R_{L1} = 20 , k\Omega$
• $R_{L2} = 20 , k\Omega$

First, calculate $R_{L1} \parallel R_{L2}$: $$ R_{L} = \frac{R_{L1} \cdot R_{L2}}{R_{L1} + R_{L2}} = \frac{20 \times 20}{20 + 20} = 10 , k\Omega $$

Now, substituting in the voltage gain formula: $$ A_v = -50 \cdot \left( \frac{10}{10} \right) = -50 $$

3. Calculate Output Resistance ($R_o'$)

Output resistance looking into the transistor can be approximated using: $$ R_o' = R $$

Where,

• $R = 200 , k\Omega$

Thus, $$ R_o' = 200 , k\Omega $$

4. Calculate Gain at Output ($A_v'$)

The output voltage gain is then: $$ A_v' = \frac{V_o}{V_{s}} $$

If $V_{s}$ is the source voltage and $V_o$ is derived as: $$ V_o = A_v \cdot V_{s} $$

Then, $$ A_v' = A_v = -50 $$

5. Calculate Inverted Current Gain ($A_i$)

The current gain is given by: $$ A_i = - \frac{I_2}{I_1} $$

Using the specific values from the circuit, where $I_1$ and $I_2$ can be calculated using Ohm's law and currents through resistors.

Let's assume these derive from a small change based on previous calculations, keeping in mind the individual transistor characteristics and provided $h_{fe}$.