For each part, determine whether the first point in the consequence \(X^{(1)}\) dominates the second point in the consequence space \(X^{(2)}\): (i) (min, max): \(X^{(1)} = (1.2, 3... For each part, determine whether the first point in the consequence \(X^{(1)}\) dominates the second point in the consequence space \(X^{(2)}\): (i) (min, max): \(X^{(1)} = (1.2, 3.5), X^{(2)} = (1.5, 3.0)\) (ii) (min, max, min): \(X^{(1)} = (10.5, 1.5, -10.0), X^{(2)} = (5.0, 0.5, -12)\) (iii) (max, max, min): \(X^{(1)} = (5, 5, 3), X^{(2)} = (2, 5, 4)\)
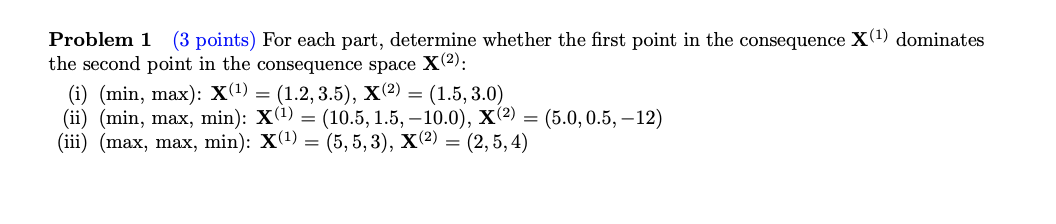
Understand the Problem
The question asks to determine if the first point [X^{(1)}] dominates the second point [X^{(2)}] in each given consequence space. The criteria for dominance depend on whether the dimensions are to be minimized or maximized, which is specified for each part.
Answer
(i) Yes (ii) No (iii) Yes
Answer for screen readers
(i) Yes (ii) No (iii) Yes
Steps to Solve
-
Analyze part (i): (min, max); $X^{(1)} = (1.2, 3.5)$, $X^{(2)} = (1.5, 3.0)$
- First dimension should be minimized: We compare the first dimension of $X^{(1)}$ and $X^{(2)}$, which are 1.2 and 1.5 respectively. Since 1.2 < 1.5, $X^{(1)}$ is better in the first dimension.
- Second dimension should be maximized: We compare the second dimension of $X^{(1)}$ and $X^{(2)}$, which are 3.5 and 3.0 respectively. Since 3.5 > 3.0, $X^{(1)}$ is better in the second dimension.
- Since $X^{(1)}$ is better than $X^{(2)}$ in both dimensions, $X^{(1)}$ dominates $X^{(2)}$.
-
Analyze part (ii): (min, max, min); $X^{(1)} = (10.5, 1.5, -10.0)$, $X^{(2)} = (5.0, 0.5, -12)$
- First dimension should be minimized: We compare the first dimension of $X^{(1)}$ and $X^{(2)}$, which are 10.5 and 5.0 respectively. Since 10.5 > 5.0, $X^{(1)}$ is worse in the first dimension.
- Second dimension should be maximized: We compare the second dimension of $X^{(1)}$ and $X^{(2)}$, which are 1.5 and 0.5 respectively. Since 1.5 > 0.5, $X^{(1)}$ is better in the second dimension.
- Third dimension should be minimized: We compare the third dimension of $X^{(1)}$ and $X^{(2)}$, which are -10.0 and -12.0 respectively. Since -10.0 > -12.0, $X^{(1)}$ is worse in the third dimension.
- $X^{(1)}$ is better in the second dimension, but worse in the first and third dimensions. Thus, $X^{(1)}$ does not dominate $X^{(2)}$.
-
Analyze part (iii): (max, max, min); $X^{(1)} = (5, 5, 3)$, $X^{(2)} = (2, 5, 4)$
- First dimension should be maximized: We compare the first dimension of $X^{(1)}$ and $X^{(2)}$, which are 5 and 2 respectively. Since 5 > 2, $X^{(1)}$ is better in the first dimension.
- Second dimension should be maximized: We compare the second dimension of $X^{(1)}$ and $X^{(2)}$, which are both 5. Thus, neither is better.
- Third dimension should be minimized: We compare the third dimension of $X^{(1)}$ and $X^{(2)}$, which are 3 and 4 respectively. Since 3 < 4, $X^{(1)}$ is better in the third dimension.
- Since $X^{(1)}$ is better or equal in all dimensions, and strictly better in at least one dimension, $X^{(1)}$ dominates $X^{(2)}$.
(i) Yes (ii) No (iii) Yes
More Information
Dominance is a fundamental concept in multi-objective optimization. A solution dominates another if it is at least as good in all objectives and strictly better in at least one objective, according to the preference (min or max) for each objective.
Tips
A common mistake is to assume that $X^{(1)}$ must be strictly better than $X^{(2)}$ in all dimensions to dominate it. $X^{(1)}$ must be at least as good as $X^{(2)}$ in all dimensions, and strictly better in one dimension to dominate.
AI-generated content may contain errors. Please verify critical information