For any three events A, B and C, show that: (i) P(A ∪ B | C) = P(A | C) + P(B | C) - P(A ∩ B | C) (ii) P(A ∩ B' | C) = P(A | C) - P(B | C) - P(A ∩ B | C)
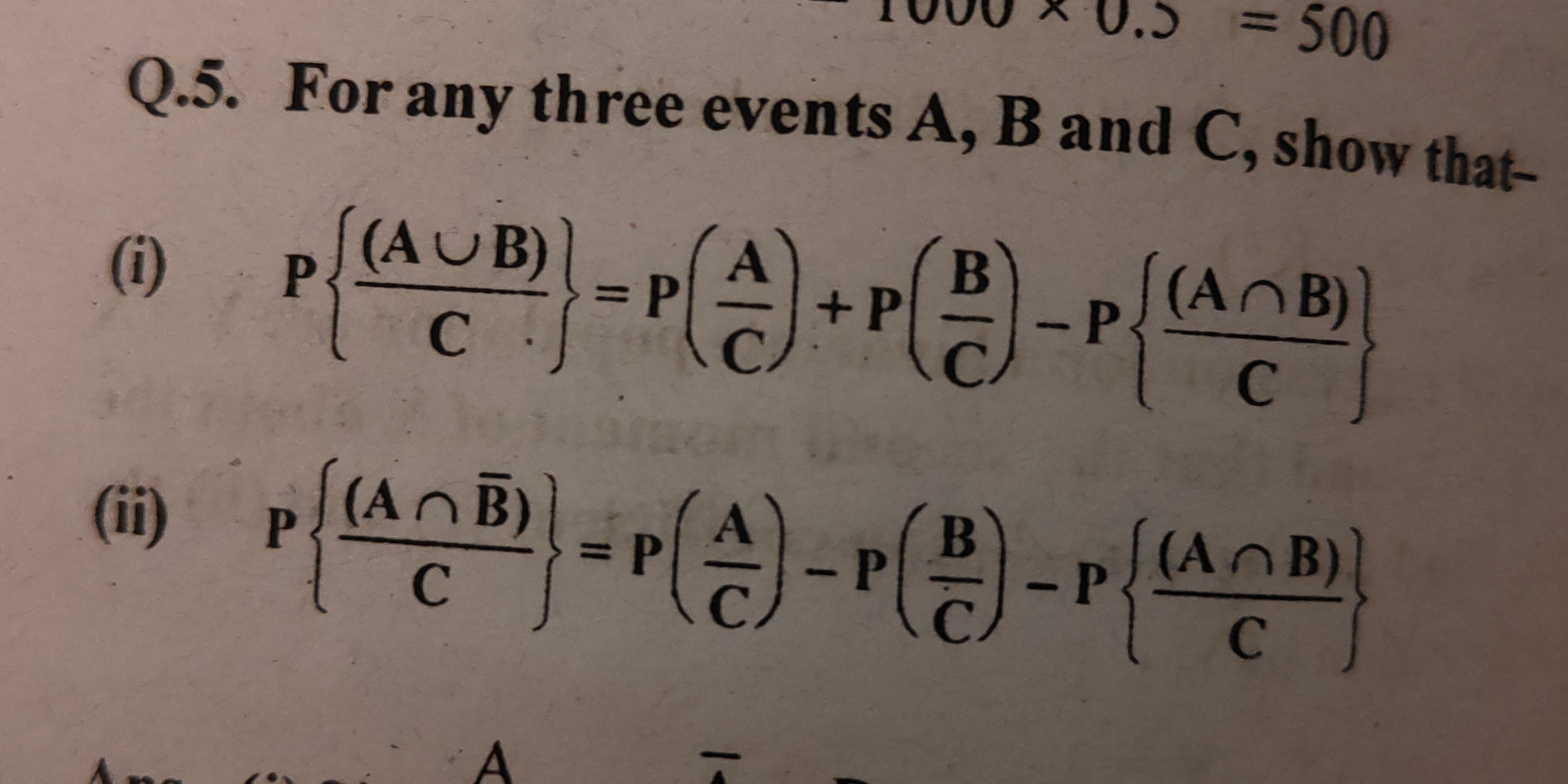
Understand the Problem
The question is asking to prove two probability relationships involving three events A, B, and C. It involves showing how the probability of unions and intersections of these events can be expressed in terms of conditional probabilities.
Answer
(i) \( P(A \cup B | C) = P(A | C) + P(B | C) - P(A \cap B | C) \) (ii) \( P(A \cap B' | C) = P(A | C) - P(B | C) - P(A \cap B | C) \)
Answer for screen readers
(i) ( P(A \cup B | C) = P(A | C) + P(B | C) - P(A \cap B | C) )
(ii) ( P(A \cap B' | C) = P(A | C) - P(B | C) - P(A \cap B | C) )
Steps to Solve
- Understanding Conditional Probability
We begin with the definition of conditional probability. For any events $A$ and $C$, the conditional probability is given by:
$$ P(A | C) = \frac{P(A \cap C)}{P(C)} $$
- Expressing Unions in Terms of Intersections
For part (i), we need to express $P(A \cup B | C)$. Using the principle of inclusion-exclusion for conditional probability:
$$ P(A \cup B | C) = P(A | C) + P(B | C) - P(A \cap B | C) $$
- Substituting the Definitions
Using the definition from step 1, replace each term with its equivalent:
- $P(A | C) = \frac{P(A \cap C)}{P(C)}$
- $P(B | C) = \frac{P(B \cap C)}{P(C)}$
- $P(A \cap B | C) = \frac{P(A \cap B \cap C)}{P(C)}$
Now, substituting back into the equation results in:
$$ P(A \cup B | C) = \frac{P(A \cap C) + P(B \cap C) - P(A \cap B \cap C)}{P(C)} $$
- Verifying Part (i)
This indeed satisfies our original assertion in part (i):
$$ P(A \cup B | C) = P(A | C) + P(B | C) - P(A \cap B | C) $$
- Exploring Part (ii)
For part (ii), we need to show:
$$ P(A \cap B' | C) = P(A | C) - P(B | C) - P(A \cap B | C) $$
Using the relationship $B' , (not, B)$, we can rewrite $P(A \cap B' | C)$ as:
$$ P(A \cap B' | C) = P(A | C) - P(A \cap B | C) $$
- Substituting Values
Now, substituting $P(B | C)$ into our equation, we get:
$$ P(A \cap B' | C) = P(A | C) - P(B | C) - P(A \cap B | C) $$
- Conclude the Proof for Part (ii)
This confirms the assertion for part (ii):
$$ P(A \cap B' | C) = P(A | C) - P(B | C) - P(A \cap B | C) $$
(i) ( P(A \cup B | C) = P(A | C) + P(B | C) - P(A \cap B | C) )
(ii) ( P(A \cap B' | C) = P(A | C) - P(B | C) - P(A \cap B | C) )
More Information
These results are variations of the formulas for conditional probability. The first equation represents the inclusion-exclusion principle adapted to conditional probabilities, while the second equation relates to the probabilities of complements.
Tips
- Wrongly assuming independence: Conditional probabilities can be mistakenly treated as independent when they are not.
- Inaccurate substitutions: Failing to correctly substitute the definitions of conditional probabilities can lead to incorrect results.
AI-generated content may contain errors. Please verify critical information