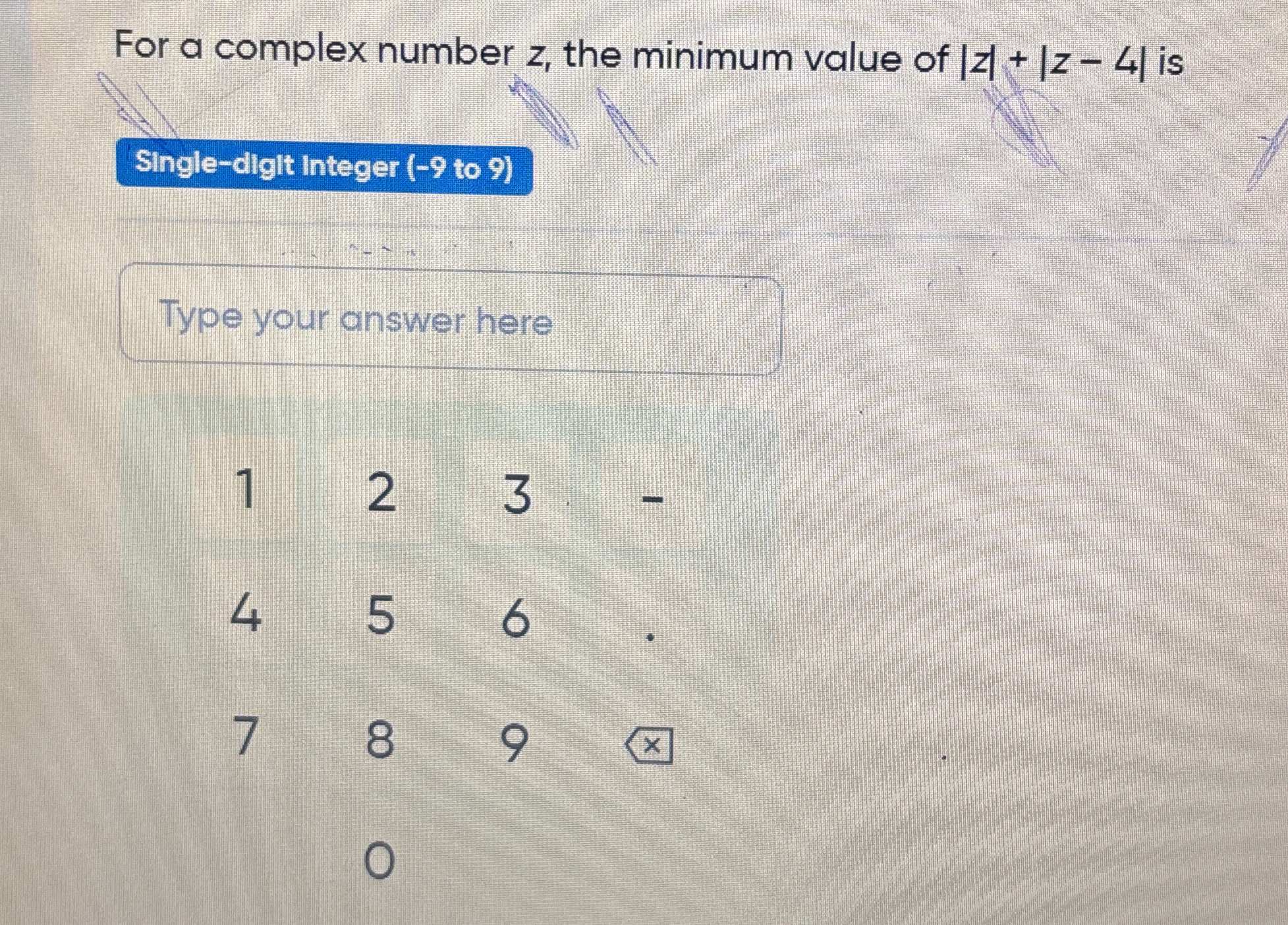
For a complex number z, the minimum value of |z| + |z - 4| is?

Steps to Solve

1. Expression Definition The expression we need to minimize is given by $$ f(z) = |z| + |z - 4| $$

2. Geometric Interpretation In the complex plane, $|z|$ represents the distance from the point $z$ to the origin (0,0) and $|z - 4|$ represents the distance from the point $z$ to the point (4,0).

3. Finding the Minimum Distance We want to find the point $z$ such that the total distance from the origin to the point (4,0) is minimized. By the triangle inequality in geometry, the shortest distance between two points occurs along a straight line.

4. Positioning of the Points The points of interest are (0,0) and (4,0). The length of the straight line connecting these two points is 4 units. Thus, when $z$ is anywhere on the segment between the origin and point (4,0), the distance remains minimal.

5. Minimum Value Calculation When $z$ is located exactly at (0,0) or (4,0), or anywhere between them along the real axis, the minimum value of $$ |z| + |z - 4| $$ is the complete span from 0 to 4, calculated as: $$ |z| + |z - 4| = 0 + 4 = 4 $$

6. Conclusion Therefore, the minimum value of the expression $$ |z| + |z - 4| $$ occurs when $z$ is any point on the line segment between these two points, and the minimal distance is 4.