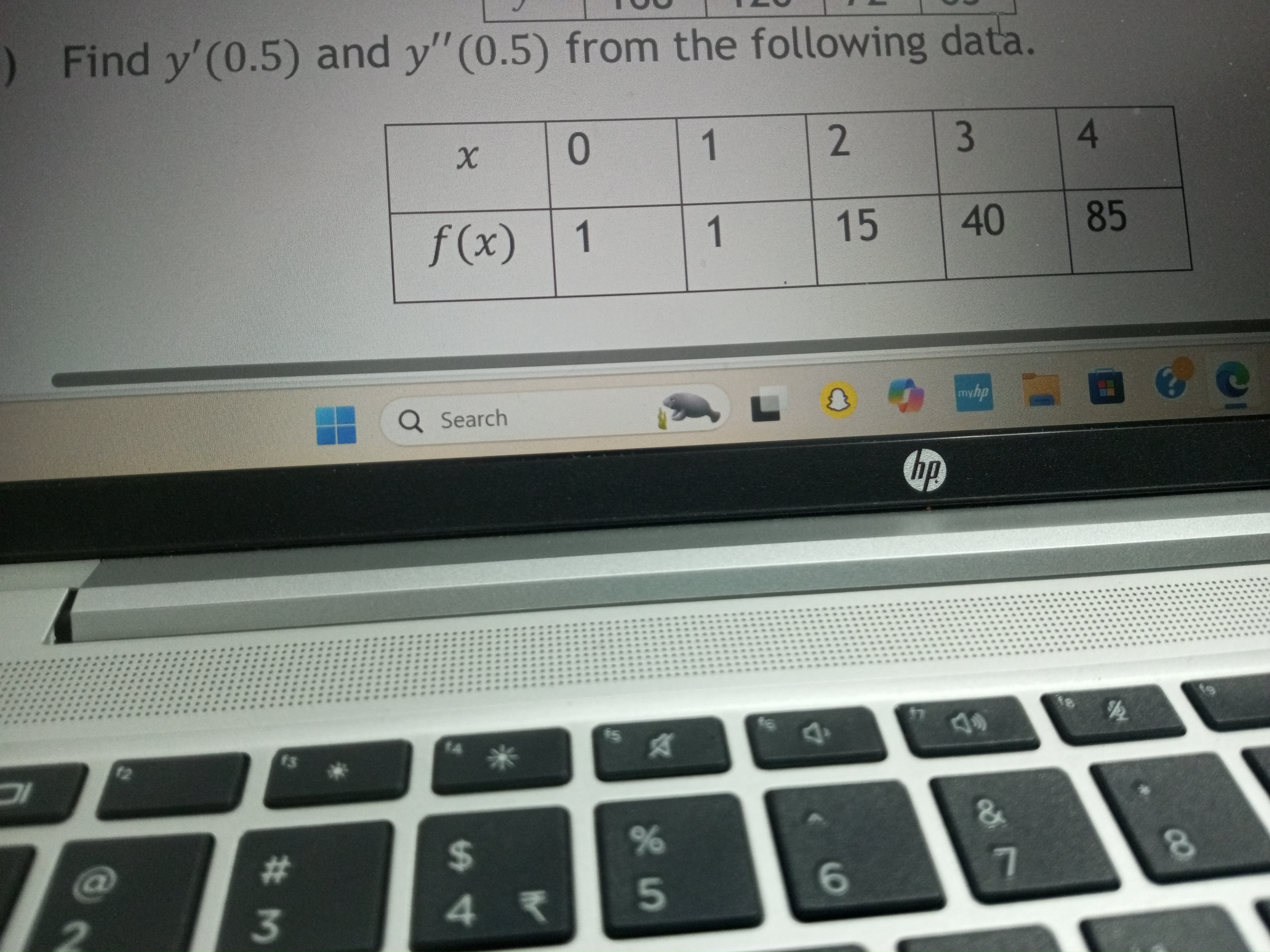
Find y'(0.5) and y''(0.5) from the following data.

Understand the Problem

The question is asking to find the first and second derivatives of a function at a specific point (0.5) using the provided data. We will use numerical differentiation techniques, specifically polynomial interpolation, as it seems necessary to estimate these derivatives from the discrete data points.

Answer

$y'(0.5) = 14$, $y''(0.5) = 11$

Steps to Solve

Set up the data points We have the following data points from the table:

[ \begin{align*} x: & \quad 0, \quad 1, \quad 2, \quad 3, \quad 4 \ f(x): & \quad 1, \quad 15, \quad 40, \quad 85 \end{align*} ]

Use finite difference for first derivative The first derivative $y'(x)$ can be estimated using the central difference formula. For the point $x = 0.5$, we will use the points $f(0)$, $f(1)$ as follows:

[ y'(0.5) \approx \frac{f(1) - f(0)}{1 - 0} = \frac{15 - 1}{1} = 14 ]

Use finite difference for second derivative The second derivative $y''(x)$ can also be estimated using finite differences. For $y''(0.5)$, we can use points $f(0)$, $f(1)$, and $f(2)$:

[ y''(0.5) \approx \frac{f(2) - 2f(1) + f(0)}{(1)^2} = \frac{40 - 2(15) + 1}{1} = 40 - 30 + 1 = 11 ]

Final results for derivatives Now we have the values for the first and second derivatives at $x = 0.5$:

[ y'(0.5) = 14 ]

[ y''(0.5) = 11 ]

The first derivative $y'(0.5) = 14$ and the second derivative $y''(0.5) = 11$.

More Information

Numerical differentiation is useful for estimating derivatives from discrete data points when an analytical function is not available. The finite difference method provides a simple and efficient way to approach this problem.

Tips

Using incorrect points for estimates: Ensure the correct adjacent points are chosen for derivative calculations.
Forgetting to simplify the expression: After calculating finite differences, remember to simplify the resulting expression.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!