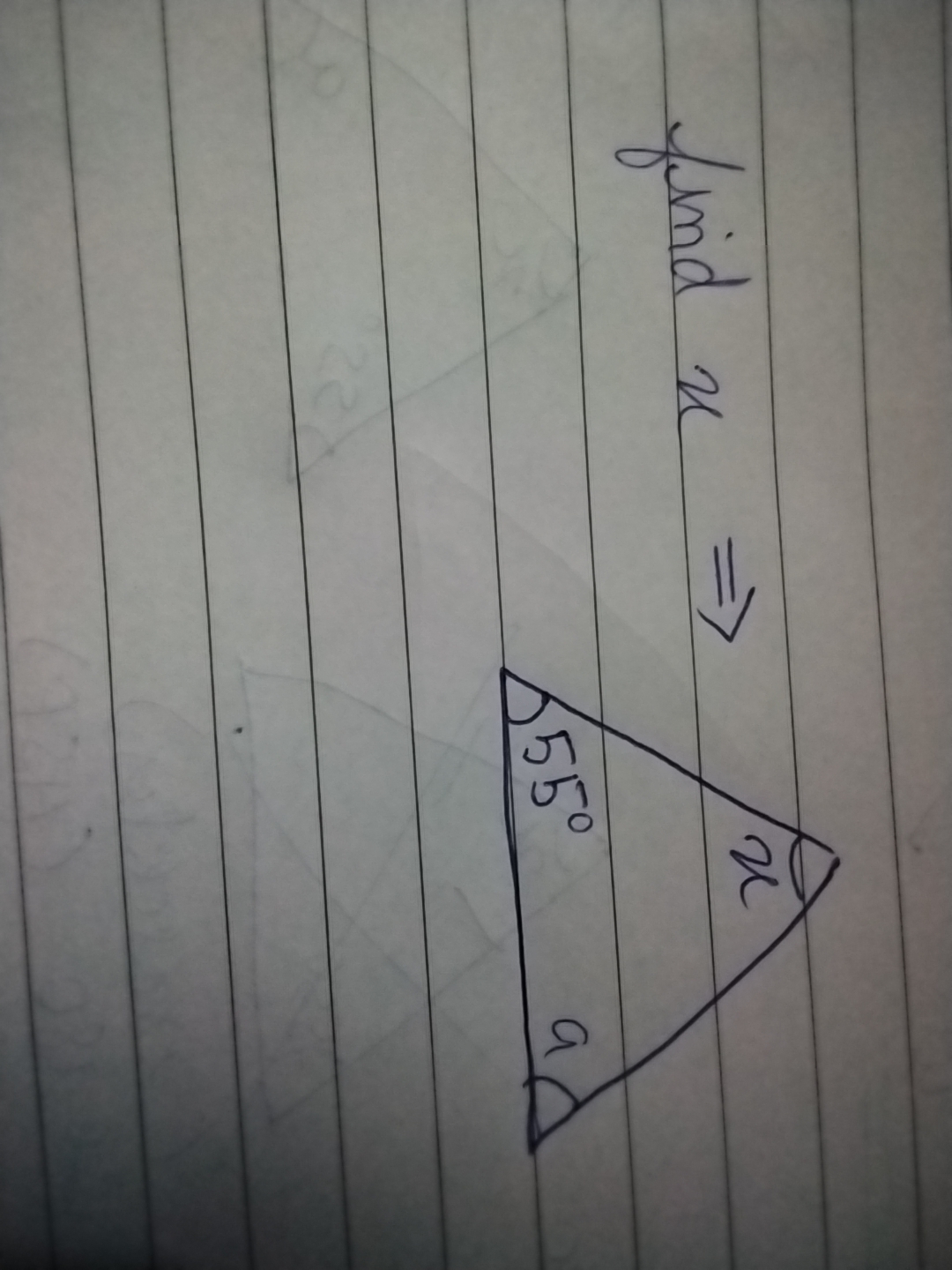
Find x in the triangle with angles 55 degrees and a.
Understand the Problem
The question is asking to find the value of 'x' in a triangle where one angle is given as 55 degrees and the other angle is labeled 'a'. We need to use the fact that the sum of the interior angles in a triangle is 180 degrees to solve for 'x'.
Answer
$x = 125^\circ - a$
Answer for screen readers
The value of $x$ is $125^\circ - a$.
Steps to Solve
- Recall the sum of angles in a triangle
The sum of the interior angles in any triangle is always $180^\circ$. Therefore, we can write the equation for the angles in the triangle:
$$ x + a + 55^\circ = 180^\circ $$
- Rearrange the equation to solve for 'x'
To isolate $x$, we can rearrange the equation:
$$ x = 180^\circ - a - 55^\circ $$
- Combine similar terms
Now we can simplify the equation:
$$ x = 180^\circ - 55^\circ - a $$
This can be simplified to:
$$ x = 125^\circ - a $$
The value of $x$ is $125^\circ - a$.
More Information
In a triangle, the relationship between angles is crucial, as they must always sum to $180^\circ$. This property helps in finding unknown angles when two angles are given.
Tips
- Forgetting the total angle sum: A common mistake is forgetting that the angles of a triangle must add up to $180^\circ$. Always remember this rule.
- Incorrectly simplifying the equation: Be careful when combining terms; ensure arithmetic is done correctly.
AI-generated content may contain errors. Please verify critical information