Find x and y based on the given angle measurements for the triangles.

Understand the Problem

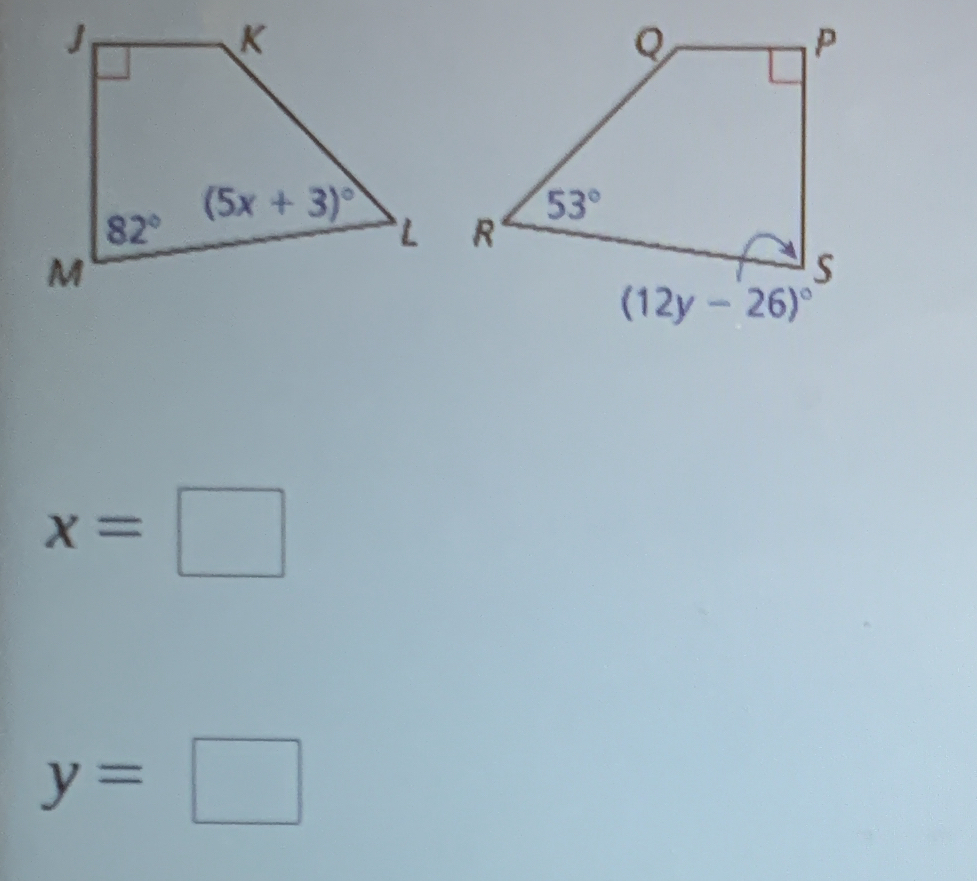
The question involves solving for the variables x and y given two geometric figures with angles expressed in terms of these variables. Specifically, we need to find the value of x using the information about triangle JKLM and the value of y from triangle QPRS, taking into account the properties of angles in a triangle.

Answer

$x = \frac{2}{5}$, $y = \frac{21}{4}$

Steps to Solve

Determine angle relationships in triangle JKLM

In triangle JKLM, the sum of angles is given by the equation: $$ 82^\circ + (5x + 3)^\circ + 90^\circ = 180^\circ $$ Here, we include the right angle (90°) and need to simplify this equation.

Simplify the equation for x

Combine the angles: $$ 175^\circ + (5x + 3)^\circ = 180^\circ $$ Subtract 175° from both sides: $$ 5x + 3 = 5 $$ Next, subtract 3 from both sides to isolate the variable term: $$ 5x = 2 $$ Finally, divide by 5: $$ x = \frac{2}{5} $$

Determine angle relationships in triangle QPRS

In triangle QPRS, the angles provide the following equation: $$ 53^\circ + (12y - 26)^\circ + 90^\circ = 180^\circ $$

Simplify the equation for y

Combine the angles: $$ 143^\circ + (12y - 26)^\circ = 180^\circ $$ Subtract 143° from both sides: $$ 12y - 26 = 37 $$ Add 26 to both sides: $$ 12y = 63 $$ Finally, divide by 12: $$ y = \frac{63}{12} = \frac{21}{4} $$

$x = \frac{2}{5}$

$y = \frac{21}{4}$

More Information

The values have been computed based on the properties of the angles in triangles. Specifically, the sum of the angles in a triangle is always 180°. The calculations for both x and y were based on setting up equations that accounted for the angles given.

Tips

Failing to recognize the right angle in triangles, leading to incorrect angle sums.
Mismanaging the addition/subtraction of terms when simplifying equations, such as neglecting to combine constants correctly.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!