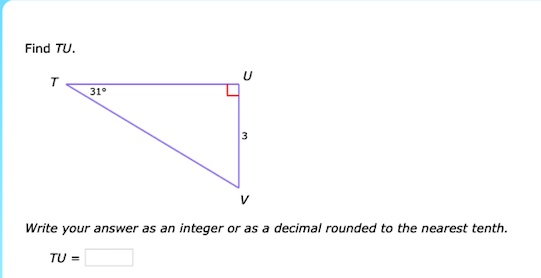
Find TU.
Understand the Problem
The question is asking to find the length of side TU in a right triangle, given one side and an angle. We can use trigonometric functions, specifically sine or cosine, to solve for TU using the known values.
Answer
TU = $2.6$
Answer for screen readers
TU = $2.6$
Steps to Solve
-
Identify the known values
In the given triangle, we have the angle $31^\circ$, the opposite side (UV) which is 3, and we need to find the adjacent side (TU). -
Choose the appropriate trigonometric function
Since we have the angle and we are looking for the side adjacent to it, we use the cosine function:
$$ \cos(\theta) = \frac{\text{adjacent}}{\text{hypotenuse}} $$ -
Set up the equation
Using the cosine of the angle, we have:
$$ \cos(31^\circ) = \frac{TU}{3} $$ -
Solve for TU
Rearranging the equation gives:
$$ TU = 3 \cdot \cos(31^\circ) $$ -
Calculate TU
Now, we calculate $TU$:
$$ TU \approx 3 \cdot 0.8572 \approx 2.5716 $$
Round to the nearest tenth:
$$ TU \approx 2.6 $$
TU = $2.6$
More Information
The solution involves using the cosine function from trigonometry, which relates the adjacent side of a right triangle to the hypotenuse.
Tips
- Forgetting to use the correct trigonometric function: Make sure to identify whether you're solving for the opposite, adjacent, or hypotenuse before choosing sine, cosine, or tangent.
- Not rounding the final answer correctly: Always double-check the rounding rules specified in the problem.
AI-generated content may contain errors. Please verify critical information