Find the values of x, y, z, and w in the following matrix equation:
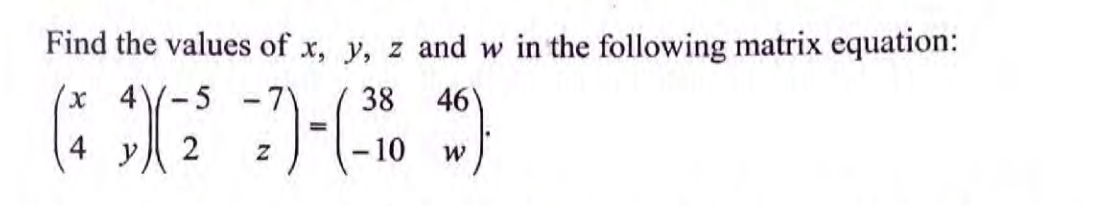
Understand the Problem
The question asks to find the values of x, y, z and w by solving the matrix equation. We will first perform matrix multiplication on the left side of the equation, and then equate the corresponding elements of the resulting matrix with the matrix on the right side of the equation to achieve the results.
Answer
$x = -6, y = 5, z = 1, w = -23$
Answer for screen readers
$x = -6$ $y = 5$ $z = 1$ $w = -23$
Steps to Solve
- Perform matrix multiplication
Multiply the two matrices on the left side of the equation: $$ \begin{pmatrix} x & 4 \ 4 & y \end{pmatrix} \begin{pmatrix} -5 & -7 \ 2 & z \end{pmatrix} = \begin{pmatrix} -5x + 8 & -7x + 4z \ -20 + 2y & -28 + yz \end{pmatrix} $$
- Equate corresponding elements
Equate the elements of the resulting matrix with the matrix on the right side: $$ \begin{pmatrix} -5x + 8 & -7x + 4z \ -20 + 2y & -28 + yz \end{pmatrix} = \begin{pmatrix} 38 & 46 \ -10 & w \end{pmatrix} $$
- Solve for x
From the equality of the top-left elements, we have $-5x + 8 = 38$. Solving for $x$: $$ -5x = 30 $$ $$ x = -6 $$
- Solve for y
From the equality of the bottom-left elements, we have $-20 + 2y = -10$. Solving for $y$: $$ 2y = 10 $$ $$ y = 5 $$
- Solve for z
From the equality of the top-right elements, we have $-7x + 4z = 46$. Substituting $x = -6$: $$ -7(-6) + 4z = 46 $$ $$ 42 + 4z = 46 $$ $$ 4z = 4 $$ $$ z = 1 $$
- Solve for w
From the equality of the bottom-right elements, we have $-28 + yz = w$. Substituting $y = 5$ and $z = 1$: $$ w = -28 + (5)(1) $$ $$ w = -28 + 5 $$ $$ w = -23 $$
$x = -6$ $y = 5$ $z = 1$ $w = -23$
More Information
The matrix equation was solved by first multiplying the two matrices, then equating corresponding elements and solving the resulting linear equations.
Tips
- Incorrect matrix multiplication: Ensure elements are multiplied and added in the correct order.
- Sign errors: Pay close attention to signs when solving linear equations.
AI-generated content may contain errors. Please verify critical information