Find the values of x and y.
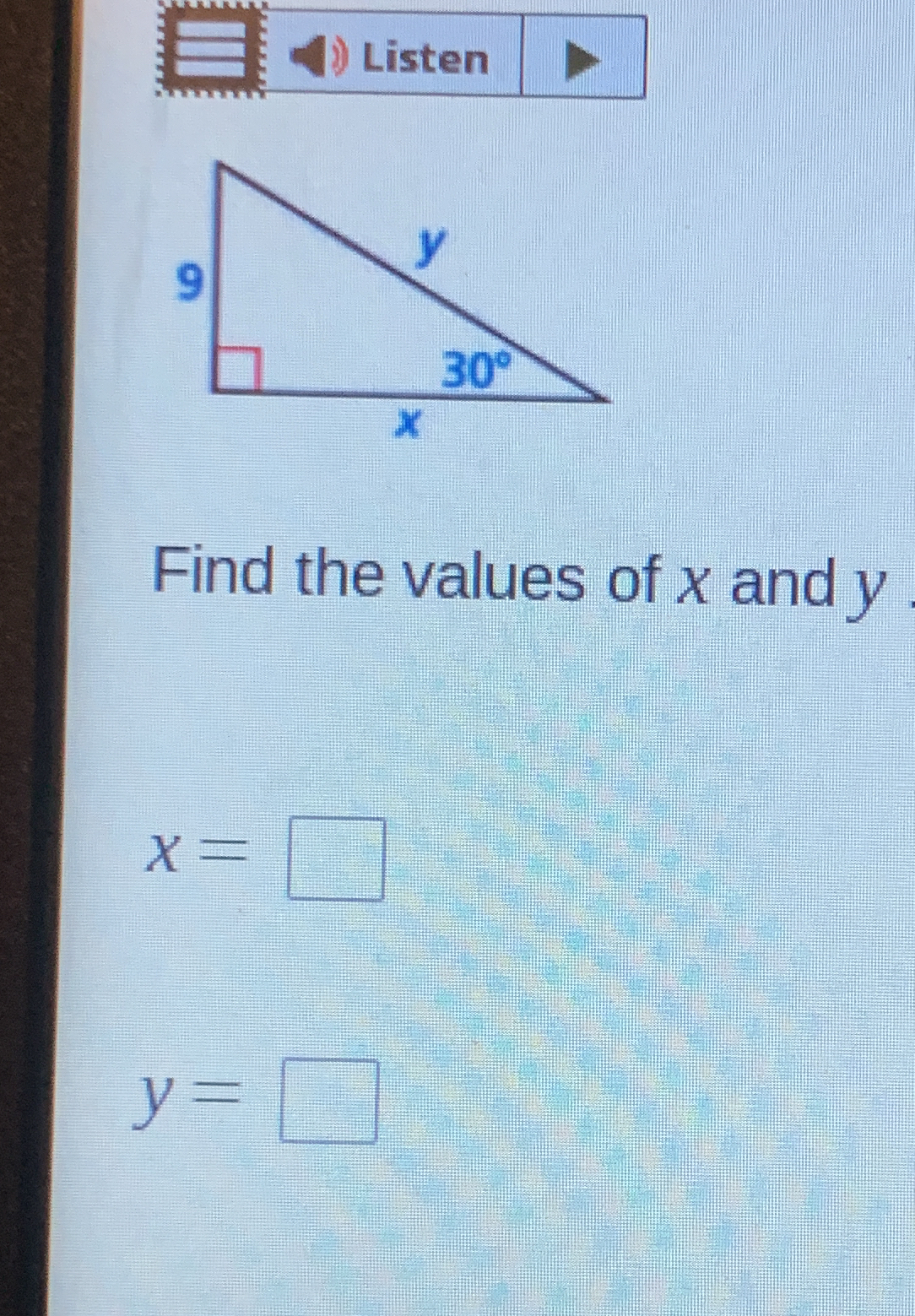
Understand the Problem
The question is asking to find the values of 'x' and 'y' in a right triangle where one angle is 30 degrees and the opposite side to the angle is 9. This involves using trigonometric ratios, specifically sine and cosine.
Answer
\( x = 9\sqrt{3}, y = 9 \)
Answer for screen readers
The values are:
- ( x = 9\sqrt{3} )
- ( y = 9 )
Steps to Solve
- Understanding the triangle components
In a right triangle with a 30-degree angle, we can identify the sides relative to the angle:
- The side opposite the 30-degree angle is 9 (this is the side labeled as "y").
- The hypotenuse is the longest side, which we will label as "h".
- The adjacent side (labeled as "x") is the side adjacent to the 30-degree angle.
- Using the sine function
To find the length of the hypotenuse "h", we can use the sine function. The sine of an angle in a right triangle is defined as the ratio of the length of the opposite side to the hypotenuse.
Using the sine function:
$$ \sin(30^\circ) = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{y}{h} $$
Substituting the known values:
$$ \sin(30^\circ) = \frac{9}{h} $$
Since $\sin(30^\circ) = \frac{1}{2}$, we can set up the equation:
$$ \frac{1}{2} = \frac{9}{h} $$
- Solving for the hypotenuse "h"
Rearranging the equation to solve for "h":
$$ h = 9 \cdot 2 = 18 $$
So, the hypotenuse "h" is 18.
- Using the cosine function to find "x"
Now we can find the adjacent side "x" using the cosine function. The cosine of the angle is given by the ratio of the adjacent side to the hypotenuse:
Using the cosine function:
$$ \cos(30^\circ) = \frac{\text{adjacent}}{\text{hypotenuse}} = \frac{x}{h} $$
Substituting the known values:
$$ \cos(30^\circ) = \frac{x}{18} $$
Since $\cos(30^\circ) = \frac{\sqrt{3}}{2}$, we can set up the equation:
$$ \frac{\sqrt{3}}{2} = \frac{x}{18} $$
- Solving for "x"
Rearranging to find "x":
$$ x = 18 \cdot \frac{\sqrt{3}}{2} = 9\sqrt{3} $$
The values are:
- ( x = 9\sqrt{3} )
- ( y = 9 )
More Information
In a right triangle, the angles and side lengths are related through trigonometric functions. The angle of 30 degrees provides specific known ratios: the sine of 30 degrees gives the relation between the opposite side and hypotenuse, while the cosine relates the adjacent side to the hypotenuse.
Tips
- Confusing sine and cosine ratios can lead to incorrect values.
- Neglecting to simplify square roots or leave them in decimal form can lead to imprecise answers.
AI-generated content may contain errors. Please verify critical information