Find the value of Z.
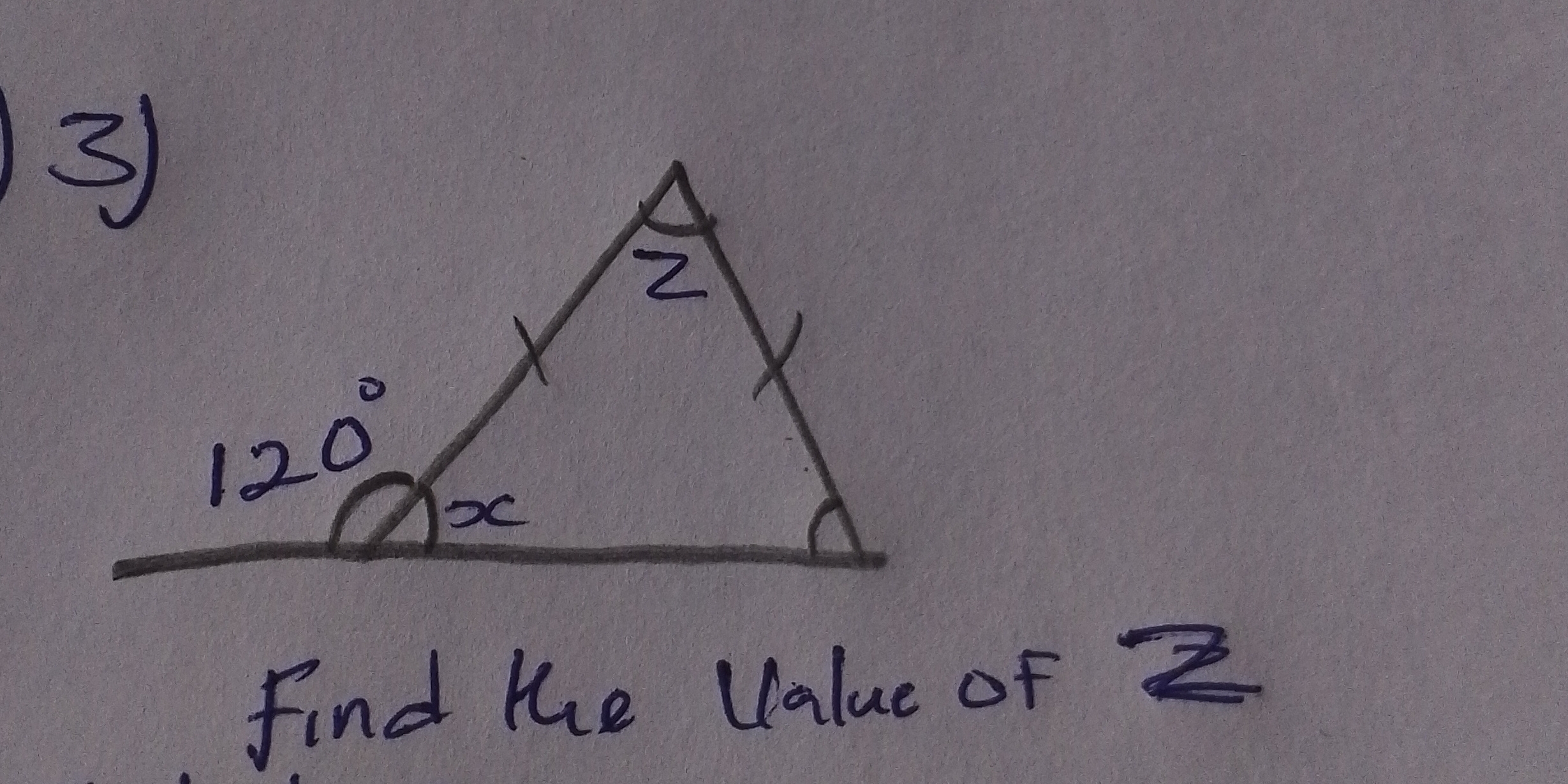
Understand the Problem
The question is asking to find the value of angle Z in a triangle where one angle is given as 120 degrees and the other is represented as X.
Answer
The value of angle $Z$ is $60^\circ - X$.
Answer for screen readers
The value of angle $Z$ is $60^\circ - X$.
Steps to Solve
-
Understand the angle sum property of a triangle The sum of all angles in a triangle is always $180^\circ$. This means we can use this property to find the unknown angle.
-
Formulate the equation Since we have one angle as $120^\circ$ and another as $X$, we can create the equation: $$ 120^\circ + X + Z = 180^\circ $$
-
Rearrange the equation to find Z To isolate $Z$, rearrange the equation: $$ Z = 180^\circ - 120^\circ - X $$
-
Simplify the equation Now, simplify the expression: $$ Z = 60^\circ - X $$
The value of angle $Z$ is $60^\circ - X$.
More Information
In this triangle, angle $Z$ depends on the value of angle $X$. If you know the value of $X$, you can directly substitute it into the equation to find $Z$. The relationship shows how changes in one angle affect the other angles in the triangle.
Tips
- Forgetting to apply the angle sum property correctly.
- Confusing the signs or substituting values incorrectly after rearranging the equation.
AI-generated content may contain errors. Please verify critical information