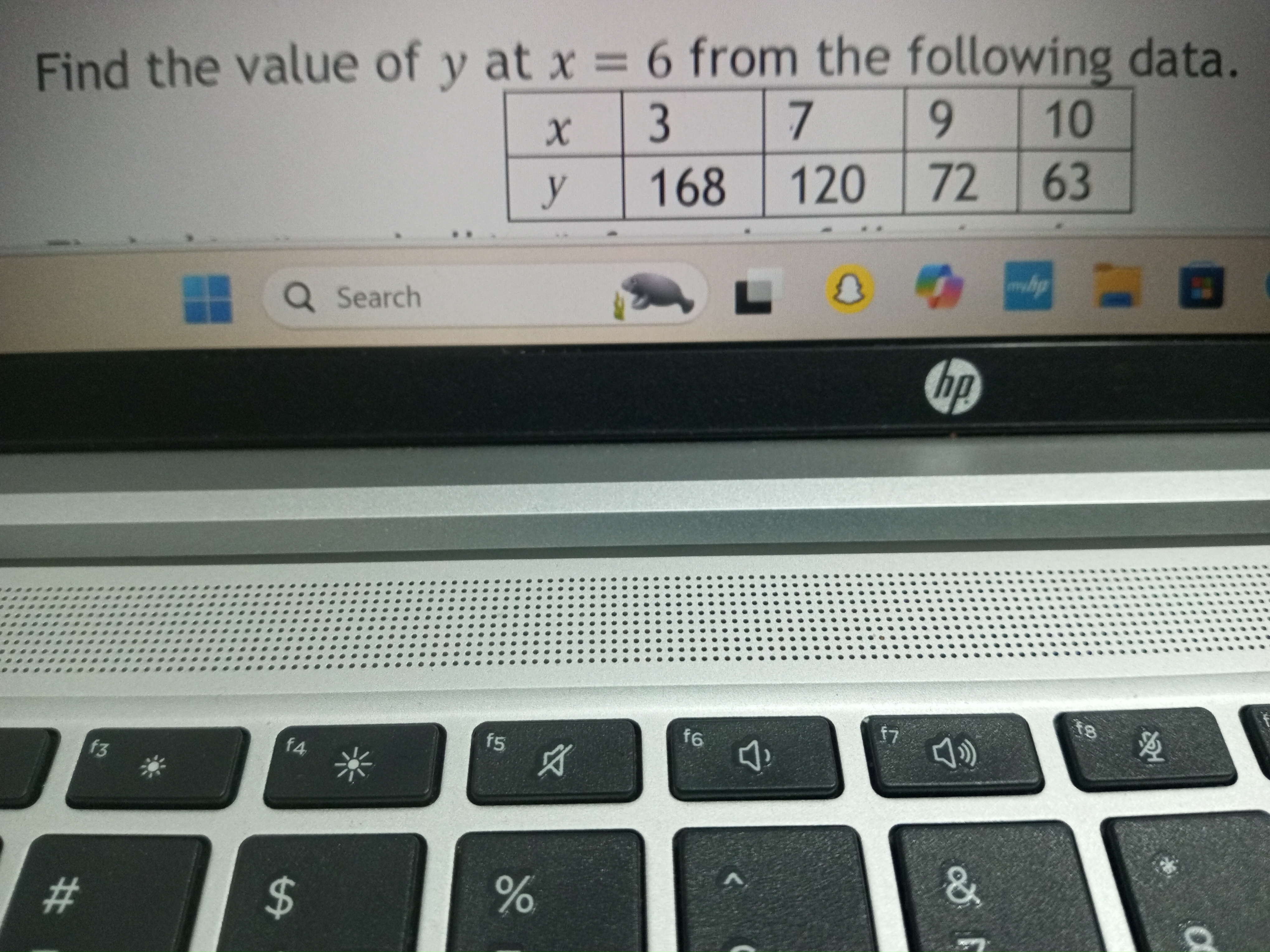
Find the value of y at x = 6 from the following data.

Understand the Problem

The question is asking to find the value of y when x is equal to 6, using the provided table of x and y values. This typically involves interpolation or extrapolation based on the given data points.

Answer

The value of $ y $ at $ x = 6 $ is $ 132 $.

Steps to Solve

Identify the data points We have the following pairs of ( (x, y) ):

( (3, 168) )
( (7, 120) )
( (9, 72) )
( (10, 63) )

We need to find ( y ) when ( x = 6 ). Since ( 6 ) is between ( 3 ) and ( 7 ), we can use linear interpolation.

Set up the linear interpolation formula The formula for linear interpolation is:

$$ y = y_1 + \frac{(x - x_1)(y_2 - y_1)}{(x_2 - x_1)} $$

Here, ( (x_1, y_1) ) is ( (3, 168) ) and ( (x_2, y_2) ) is ( (7, 120) ).

Substitute the known values Now, substituting the values into the formula:

( x = 6 ), ( x_1 = 3 ), ( y_1 = 168 ), ( x_2 = 7 ), ( y_2 = 120 ):

$$ y = 168 + \frac{(6 - 3)(120 - 168)}{(7 - 3)} $$

Calculate the result First, calculate the difference in ( y ):

$$ 120 - 168 = -48 $$

Now plug it back into the equation:

$$ y = 168 + \frac{(3)(-48)}{4} $$

Calculating the fraction:

$$ y = 168 + \frac{-144}{4} = 168 - 36 = 132 $$

The value of ( y ) at ( x = 6 ) is ( 132 ).

More Information

The linear interpolation method allows us to estimate values that fall between two known data points. It's widely used in various fields such as finance and science.

Tips

Forgetting to check if the ( x ) value lies between the known ( x ) values.
Failing to use the correct points for interpolation, which can lead to incorrect results.
Miscalculating the fraction or adjustments based on linear interpolation.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!