Find the value of m + 5n / m - 5n, find the value of x - 6a / x + 6b, find the value of x - 3y / x + 3z - x - 3z.

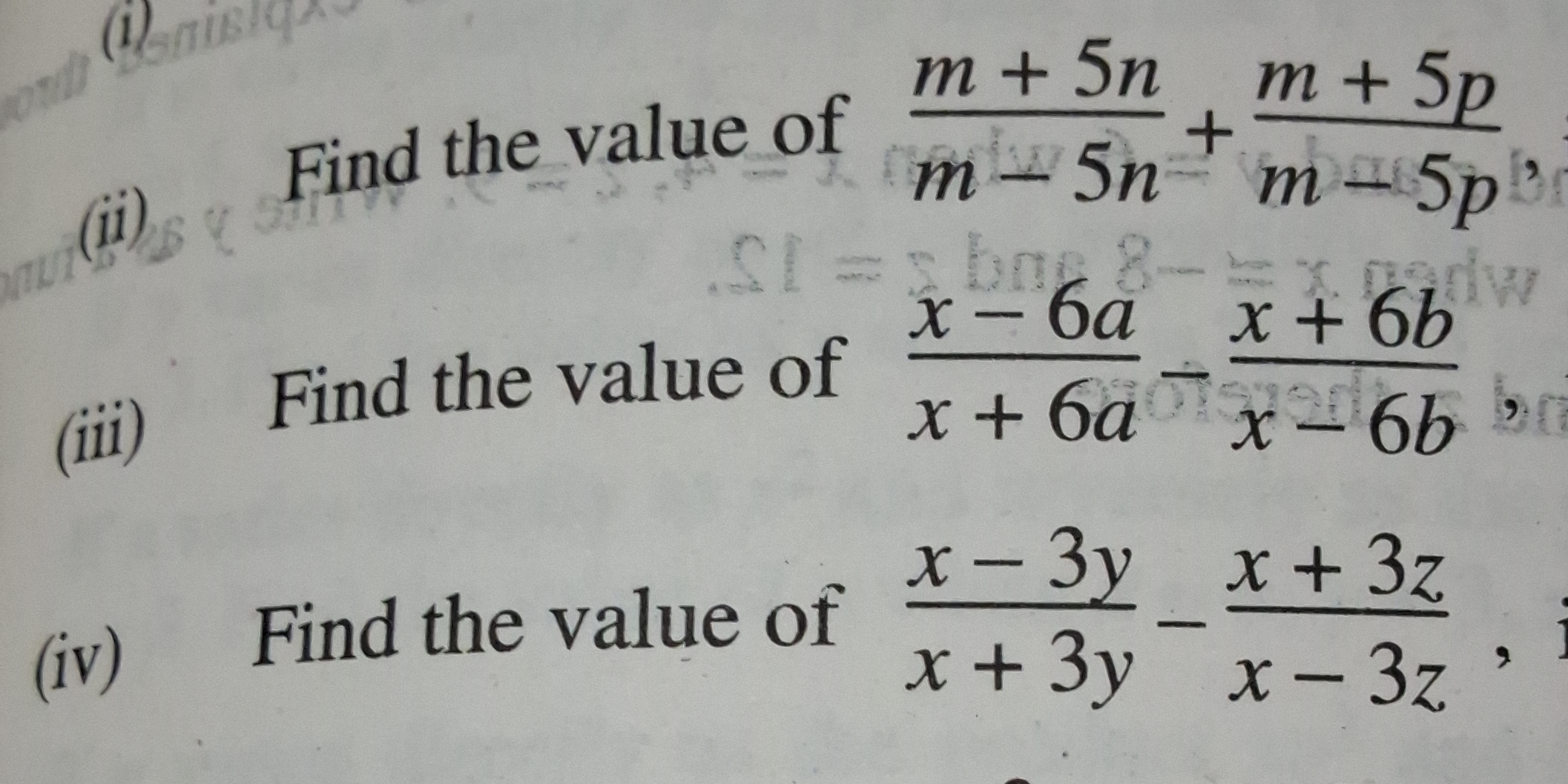
Understand the Problem

The question is asking to find the value of certain algebraic expressions involving variables and constants as shown in the image. Each expression requires solving for a particular ratio or comparison, which involves performing algebraic manipulation.

Answer

1. $\frac{m + 5n}{m - 5n}$; 2. $\frac{x - 6a}{x + 6b}$; 3. $\frac{-3(y + z)}{x + 3z}$.

Steps to Solve

Solve the first expression: $\frac{m + 5n}{m - 5n}$

This expression is already simplified, so we can just write it down as it is for any specific values assigned to $m$ and $n$.
Solve the second expression: $\frac{x - 6a}{x + 6b}$

This expression is also in its simplest form. It can be evaluated if values of $x$, $a$, and $b$ are known.
Solve the third expression: $\frac{x - 3y}{x + 3z} - \frac{x - 3z}{x - 3z}$

First, notice that $\frac{x - 3z}{x - 3z} = 1$ (as long as $x \neq 3z$), so we can rewrite the expression as: $$ \frac{x - 3y}{x + 3z} - 1 $$

To combine these, we need a common denominator: $$ \frac{x - 3y - (x + 3z)}{x + 3z} $$
Combine and simplify

This gives: $$ \frac{x - 3y - x - 3z}{x + 3z} = \frac{-3y - 3z}{x + 3z} $$

Rewrite it as: $$ \frac{-3(y + z)}{x + 3z} $$

The values of the expressions are:

$\frac{m + 5n}{m - 5n}$ (depends on $m$ and $n$).
$\frac{x - 6a}{x + 6b}$ (depends on $x$, $a$, and $b$).
$\frac{-3(y + z)}{x + 3z}$.

More Information

The results from these algebraic expressions depend on the values assigned to the variables $m$, $n$, $x$, $a$, $b$, $y$, and $z$. The expressions illustrate simple algebraic manipulation techniques including combining fractions and simplifying.

Tips

Forgetting to simplify fractions when the numerator has similar terms.
Not recognizing that dividing by similar terms results in 1.
Failing to rewrite expressions correctly when combining them.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!