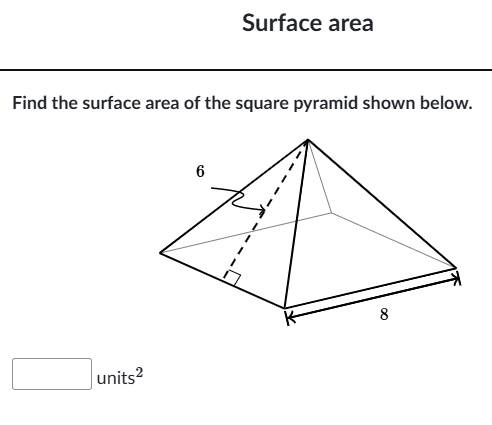
Find the surface area of the square pyramid shown below.
Understand the Problem
The question is asking us to find the surface area of a square pyramid with a base length of 8 units and a slant height of 6 units. To solve this, we will use the formula for the surface area of a pyramid, which includes the area of the base and the area of the triangular sides.
Answer
$160$ units$^2$
Answer for screen readers
The surface area of the square pyramid is $160$ units$^2$.
Steps to Solve
- Calculate the area of the base
The base of the square pyramid is a square with a side length of 8 units.
The area $A_{base}$ of the square base is calculated using the formula:
$$ A_{base} = \text{side}^2 = 8^2 = 64 \text{ units}^2 $$
- Calculate the area of one triangular face
Each triangular face has a base of 8 units and a height equal to the slant height of the pyramid, which is 6 units.
The area $A_{triangle}$ of one triangular face is given by:
$$ A_{triangle} = \frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times 8 \times 6 = 24 \text{ units}^2 $$
- Calculate the total area of the triangular faces
Since there are four identical triangular faces, the total area of the triangular faces $A_{triangular\ faces}$ is:
$$ A_{triangular\ faces} = 4 \times A_{triangle} = 4 \times 24 = 96 \text{ units}^2 $$
- Calculate the total surface area
The total surface area $A_{total}$ of the pyramid is the sum of the area of the base and the area of the triangular faces:
$$ A_{total} = A_{base} + A_{triangular\ faces} = 64 + 96 = 160 \text{ units}^2 $$
The surface area of the square pyramid is $160$ units$^2$.
More Information
The surface area of a pyramid combines both the base area and the lateral surface area from the triangular sides. The formula is useful in various real-world applications, such as architecture and design.
Tips
- Confusing slant height with the vertical height: The slant height is not the same as the height of the pyramid from the base to the apex.
- Forgetting to calculate the total area of all triangular faces: Remember to multiply the area of one face by the number of faces.
AI-generated content may contain errors. Please verify critical information