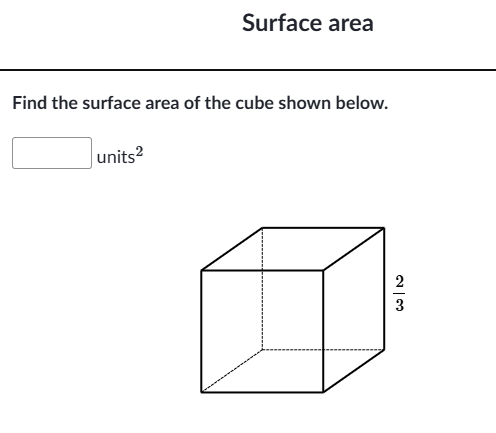
Find the surface area of the cube shown below.
Understand the Problem
The question is asking to calculate the surface area of a cube given the length of its sides. The side length is provided as a fraction, specifically 2/3 units. The surface area can be calculated using the formula 6 * (side length)².
Answer
The surface area of the cube is $\frac{8}{3}$ units².
Answer for screen readers
The surface area of the cube is $\frac{8}{3}$ units².
Steps to Solve
-
Identify the side length of the cube The length of each side of the cube is given as $\frac{2}{3}$ units.
-
Apply the surface area formula The surface area $A$ of a cube can be calculated using the formula: $$ A = 6 \times (\text{side length})^2 $$
-
Substitute the side length into the formula Now substitute $\frac{2}{3}$ for the side length: $$ A = 6 \times \left(\frac{2}{3}\right)^2 $$
-
Calculate the square of the side length First calculate $\left(\frac{2}{3}\right)^2$: $$ \left(\frac{2}{3}\right)^2 = \frac{4}{9} $$
-
Multiply by 6 Now multiply by 6: $$ A = 6 \times \frac{4}{9} = \frac{24}{9} $$
-
Simplify the fraction Simplify $\frac{24}{9}$ to its simplest form: $$ \frac{24}{9} = \frac{8}{3} $$
The surface area of the cube is $\frac{8}{3}$ units².
More Information
The surface area of a cube increases with the square of the side length, meaning small changes in side length can significantly affect the overall area. In practical terms, this may relate to surface treatments or materials used.
Tips
- Forgetting to square the side length: Many students may skip the squaring step and just multiply by 6.
- Incorrectly simplifying fractions: Ensure you simplify your final answer properly.
AI-generated content may contain errors. Please verify critical information