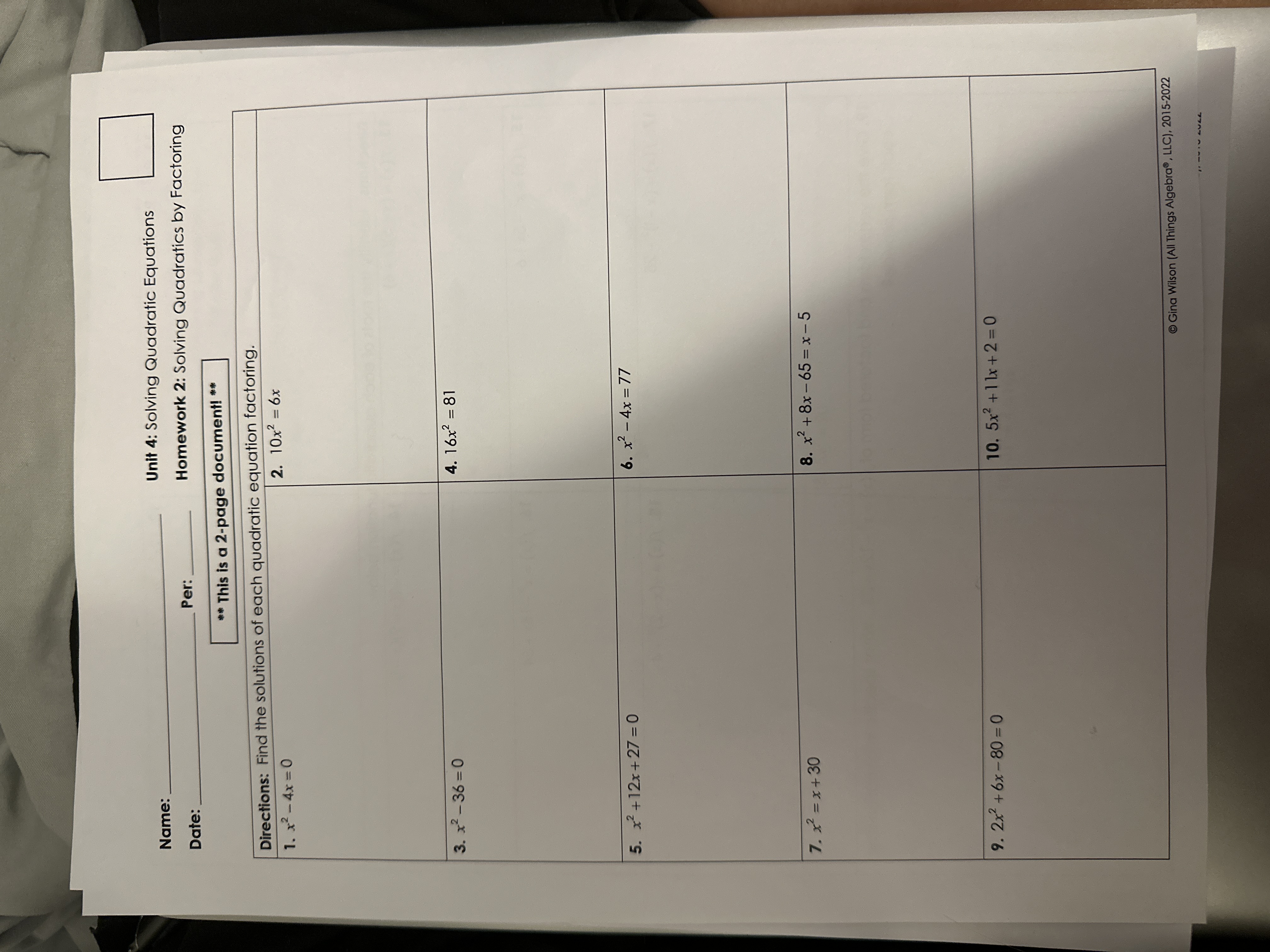
Find the solutions of each quadratic equation factoring.

Understand the Problem

The question is asking for the solutions to several quadratic equations by factoring. Each equation requires the identification of factors leading to solutions for the variable.

Answer

The solutions to the equations are as follows: 1. \( x = 0, 4 \) 2. \( x = 0, 0.6 \) 3. \( x = 6, -6 \) 4. \( x = \frac{9}{4}, -\frac{9}{4} \) 5. \( x = -1, 3 \) 6. \( x = -5, 13 \) 7. \( x = 5, -6 \) 8. \( x = -13, 5 \) 9. \( x = 5, -8 \) 10. \( x = -\frac{2}{5}, -1 \)

Steps to Solve

Set the equation to zero

For each quadratic equation, we need to rearrange it so that one side equals zero. This is done where necessary.

Factor the quadratic equation

Once in standard form ( ax^2 + bx + c = 0 ), identify two numbers that multiply to ( ac ) (product) and add to ( b ) (sum). This will allow us to factor the equation.

Create two binomials

Rewrite the quadratic equation in factored form ( (px + q)(rx + s) = 0 ). Set each factor equal to zero to find the potential solutions.

Solve for the variable

Solve each factor from the previous step to find the solutions for ( x ).

Check your solutions

Substitute your solutions back into the original equation to verify they satisfy the equation.

( x(x - 4) = 0 ) → ( x = 0, x = 4 )
( 10x(x - 0.6) = 0 ) → ( x = 0, x = 0.6 )
( (x - 6)(x + 6) = 0 ) → ( x = 6, x = -6 )
( (4x - 9)(4x + 9) = 0 ) → ( x = \frac{9}{4}, x = -\frac{9}{4} )
( (x + 1)(x - 3) = 0 ) → ( x = -1, x = 3 )
( (x + 5)(x - 13) = 0 ) → ( x = -5, x = 13 )
( (x - 5)(x + 6) = 0 ) → ( x = 5, x = -6 )
( (x + 13)(x - 5) = 0 ) → ( x = -13, x = 5 )
( (2x - 10)(x + 8) = 0 ) → ( x = 5, x = -8 )
( (5x + 2)(x + 1) = 0 ) → ( x = -\frac{2}{5}, x = -1 )

More Information

Factoring quadratic equations can often reveal solutions quickly. Some equations factor nicely while others may require methods like completing the square or using the quadratic formula if factoring is not straightforward. Understanding the relationship between the coefficients in the quadratic equation can simplify the factoring process.

Tips

Failing to set the equation equal to zero before factoring. Always ensure one side equals zero.
Not correctly identifying the factors that multiply and add to the right constants. Practice finding pairs of numbers that meet both conditions.
Forgetting to check the solutions by substituting them back into the original equation can lead to accepting false solutions.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!