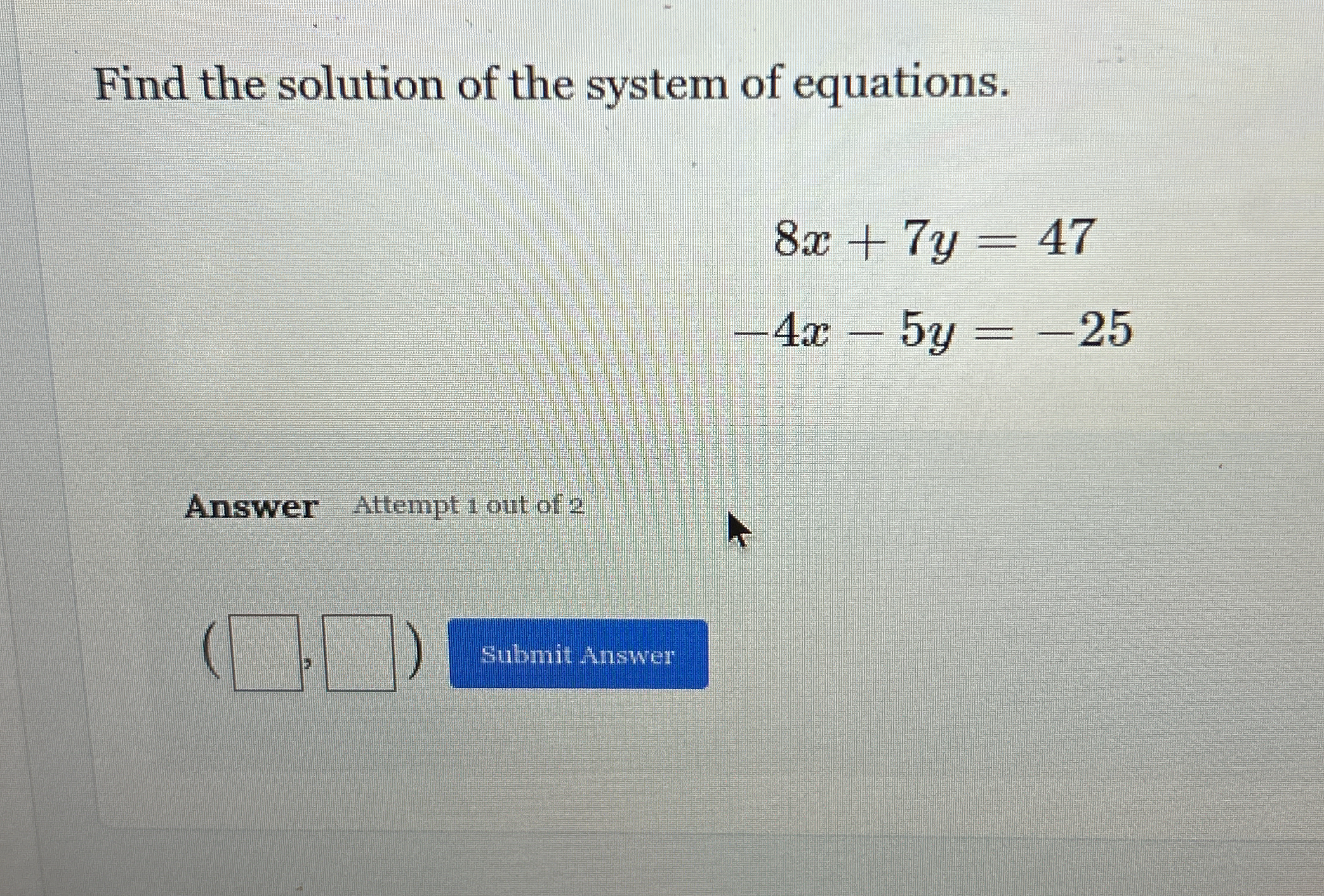
Find the solution of the system of equations: 8x + 7y = 47, -4x - 5y = -25.

Understand the Problem

The question is asking to find the solution of a system of equations involving two variables, x and y. The provided equations are linear, and the goal is to determine the values of x and y that satisfy both equations simultaneously.

Answer

The solution is \( (5, 1) \).

Steps to Solve

Write down the equations

The given system of equations is:

[ 8x + 7y = 47 ] [ -4x - 5y = -25 ]

Rearrange the first equation

We can solve the first equation for (y):

[ 7y = 47 - 8x ] [ y = \frac{47 - 8x}{7} ]

Substitute y in the second equation

Now, substitute (y) into the second equation:

[ -4x - 5\left(\frac{47 - 8x}{7}\right) = -25 ]

Clear the fraction

Multiply the entire equation by 7 to eliminate the fraction:

[ -28x - 5(47 - 8x) = -175 ]

Distribute and simplify

Distribute -5:

[ -28x - 235 + 40x = -175 ]

Combine like terms:

[ 12x - 235 = -175 ]

Isolate x

Add 235 to both sides:

[ 12x = 60 ] Then divide by 12:

[ x = 5 ]

Find y using x

Now substitute (x = 5) back into the equation for (y):

[ y = \frac{47 - 8(5)}{7} ] [ y = \frac{47 - 40}{7} = \frac{7}{7} = 1 ]

The solution to the system of equations is ( (5, 1) ).

More Information

The provided system of equations involves two linear equations. The intersection point of these lines gives the values of (x) and (y) that satisfy both equations simultaneously.

Tips

Forgetting to clear the fraction when substituting (y) into the second equation.
Not combining like terms correctly, leading to an incorrect value of (x).

AI-generated content may contain errors. Please verify critical information

Thank you for voting!