Find the solution of the system of equations: -8x + 7y = -2 and -8x + 8y = 8.
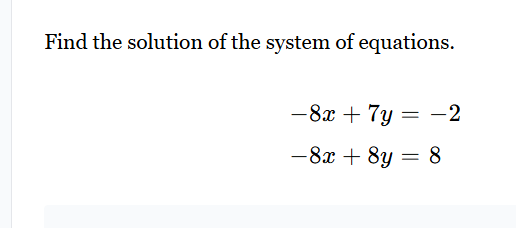
Understand the Problem
The question is asking for the solution to a system of two linear equations. We will solve for the values of x and y that satisfy both equations simultaneously.
Answer
The solution is $(x, y) = (9, 10)$.
Answer for screen readers
The solution to the system of equations is: $$ (x, y) = (9, 10) $$
Steps to Solve
- Set up the equations
The two equations given are: $$ -8x + 7y = -2 \quad (1) $$ $$ -8x + 8y = 8 \quad (2) $$
- Eliminate $x$ by subtracting the equations
To eliminate $x$, we can subtract equation (1) from equation (2): $$ (-8x + 8y) - (-8x + 7y) = 8 - (-2) $$ This simplifies to: $$ y = 10 $$
- Substitute $y$ back into one of the original equations
Now substitute $y = 10$ into equation (1): $$ -8x + 7(10) = -2 $$ This simplifies to: $$ -8x + 70 = -2 $$
- Solve for $x$
Rearranging the equation gives: $$ -8x = -2 - 70 $$ $$ -8x = -72 $$ Dividing both sides by -8: $$ x = 9 $$
The solution to the system of equations is: $$ (x, y) = (9, 10) $$
More Information
In this problem, we used the method of elimination to solve a system of linear equations. The results tell us that both equations intersect at the point (9, 10).
Tips
- Forgetting to distribute: When substituting values, ensure all terms are correctly simplified.
- Confusing signs: Pay close attention to negative and positive signs when subtracting or moving terms.
AI-generated content may contain errors. Please verify critical information