Find the solution of the differential equation that satisfies the given initial condition: du/dt = (2t + sec^2 t) / (2u), u(0) = -5.
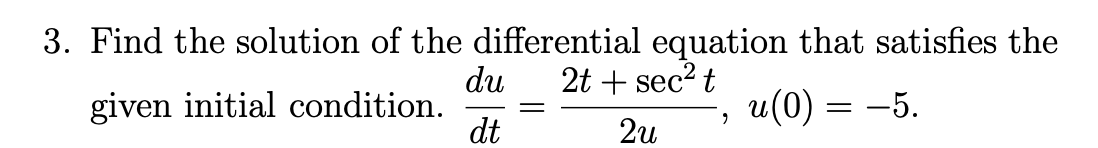
Understand the Problem
The question is asking to find the solution to a specific differential equation with a given initial condition. To solve it, we will employ techniques for solving first-order differential equations.
Answer
The solution is \( u(t) = -\sqrt{t^2 + \tan t + 25} \).
Answer for screen readers
The solution to the differential equation is
$$ u(t) = -\sqrt{t^2 + \tan t + 25} $$
Steps to Solve
-
Rearrange the equation
Start with the given differential equation: $$ \frac{du}{dt} = \frac{2t + \sec^2 t}{2u} $$
Multiply both sides by ( 2u ): $$ 2u \frac{du}{dt} = 2t + \sec^2 t $$
-
Separate the variables
Rewrite the equation to separate variables ( u ) and ( t ): $$ 2u , du = (2t + \sec^2 t) , dt $$
-
Integrate both sides
Integrate both sides: $$ \int 2u , du = \int (2t + \sec^2 t) , dt $$
The left side integrates to: $$ u^2 + C_1 $$
The right side integrates to: $$ t^2 + \tan t + C_2 $$
Combine the constants: $$ u^2 = t^2 + \tan t + C $$
-
Apply the initial condition
Use the initial condition ( u(0) = -5 ): $$ (-5)^2 = 0^2 + \tan(0) + C $$ $$ 25 = C $$
This gives us: $$ u^2 = t^2 + \tan t + 25 $$
-
Solve for ( u )
Taking the square root gives us the general solution: $$ u = -\sqrt{t^2 + \tan t + 25} $$
We take the negative root because ( u(0) = -5 ).
The solution to the differential equation is
$$ u(t) = -\sqrt{t^2 + \tan t + 25} $$
More Information
This differential equation describes a relationship where the rate of change of ( u ) depends non-linearly on both ( t ) and ( u ). The negative root is chosen based on the given initial condition, ensuring the function agrees with the specified ( u(0) = -5 ).
Tips
- Forgetting to apply the initial condition correctly: Ensure that the correct value of ( u(0) ) is used when solving for the constant ( C ).
- Misapplying the square root: Be cautious to consider negative roots when the initial condition specifies a negative value for ( u ).
AI-generated content may contain errors. Please verify critical information