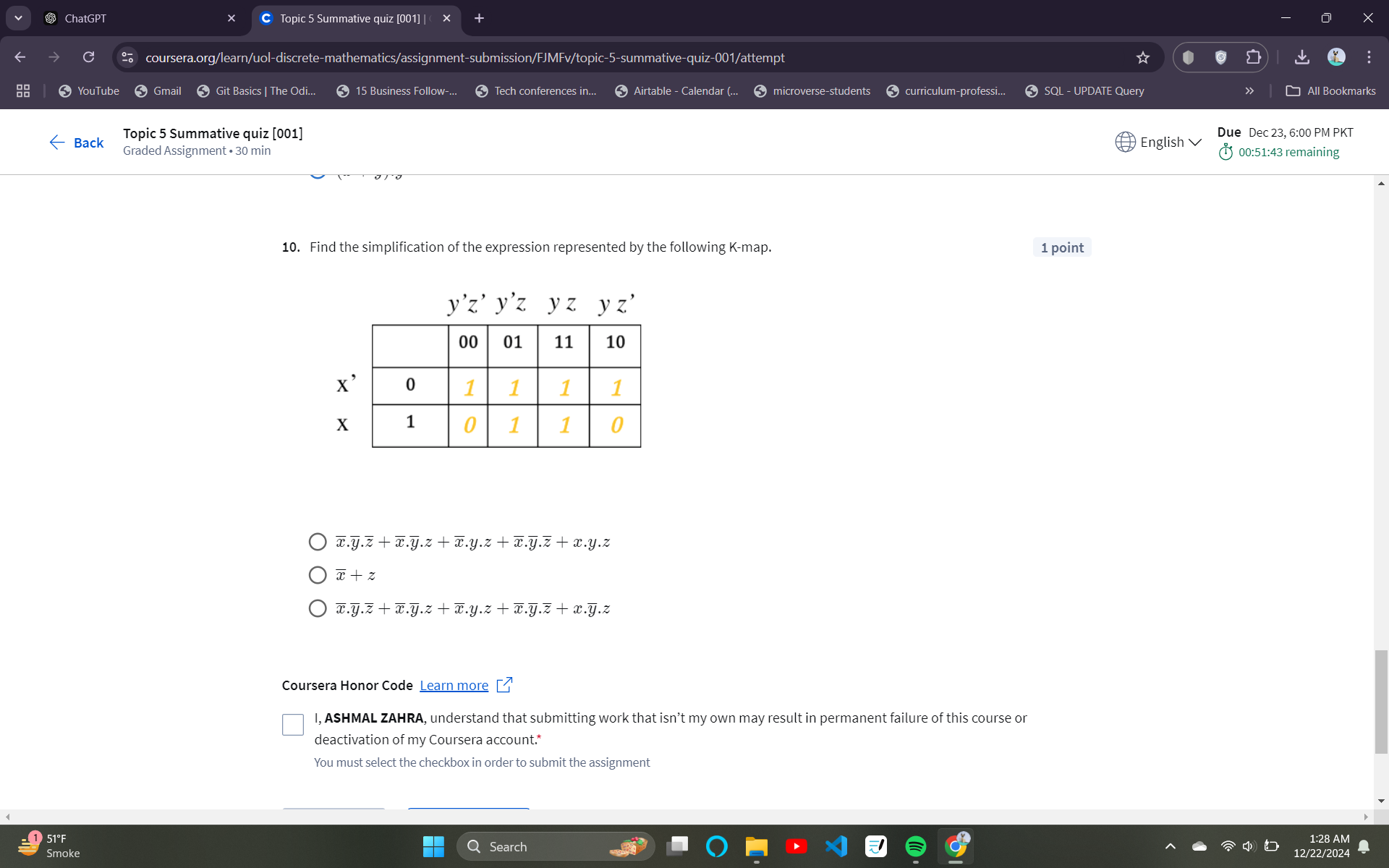
Find the simplification of the expression represented by the following K-map.

Understand the Problem

The question requires finding the simplification of a Boolean expression represented by a K-map (Karnaugh map). It involves logical reasoning and manipulation of Boolean algebra to reduce the expression to its simplest form.

Answer

The simplified expression is $ x' + yz $.

Steps to Solve

Identify the K-map values The K-map provided has the following values:
- For ( x'y' ):
  - ( y'z' ) (00): 1
  - ( y'z ) (01): 1
  - ( yz ) (11): 1
  - ( yz' ) (10): 0
- For ( xy' ):
  - ( y'z' ) (00): 0
  - ( y'z ) (01): 1
  - ( yz ) (11): 1
  - ( yz' ) (10): 0
Group the 1s in K-map We will group 1s as follows:
- The first horizontal group covers the three 1s in the first row: ( x'y'z' ), ( x'y'z ), and ( x'yz ), which simplify to ( x' ).
- The second group covers the two 1s in the second column: ( xy'z ) and ( xyz ) which simplifies to ( yz ).
Write the simplified expression Combining the results from the groups, the overall simplified expression is: $$ x' + yz $$

The simplified expression is ( x' + yz ).

More Information

Karnaugh maps are a visual method for simplifying Boolean expressions. They allow for easy identification of grouping possibilities based on adjacent cells, providing a straightforward path to minimization.

Tips

Failing to correctly identify all possible groups, especially overlooking larger groups which can lead to a more simplified expression.
Not noting that adjacent 1s can wrap around the edges of the K-map if they are in the same column/row.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!