Find the quadratic equation with the roots (α² - β²) = 3 and α - β = 2.
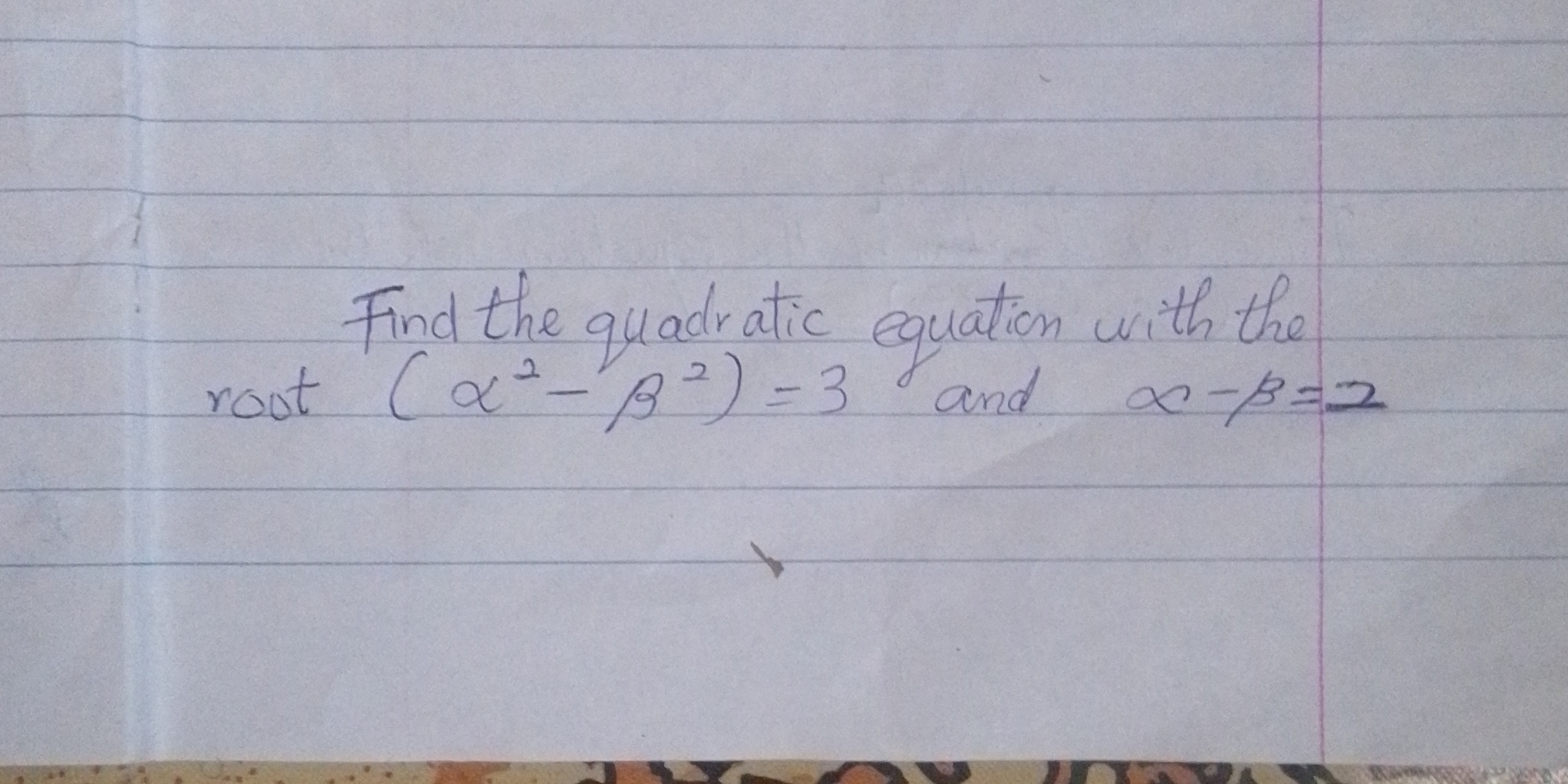
Understand the Problem
The question is asking to find a quadratic equation given two conditions involving the roots α and β. One condition states that the difference of their squares is 3, and the other states that their difference is 2.
Answer
The quadratic equation is $$ 16x^2 - 24x + 7 = 0 $$
Answer for screen readers
The quadratic equation is
$$ 16x^2 - 24x + 7 = 0 $$
Steps to Solve
-
Identify the equations We have two conditions involving the roots $\alpha$ and $\beta$:
- The difference of their squares: $$ \alpha^2 - \beta^2 = 3 $$
- Their difference: $$ \alpha - \beta = 2 $$
-
Use the difference of squares formula The difference of squares can be factored as: $$ \alpha^2 - \beta^2 = (\alpha - \beta)(\alpha + \beta) $$ Substituting the value of $\alpha - \beta$: $$ 3 = 2(\alpha + \beta) $$
-
Solve for $\alpha + \beta$ Now, isolate $\alpha + \beta$: $$ \alpha + \beta = \frac{3}{2} $$
-
Set up the quadratic equation Now we have:
- The sum of the roots: $s = \alpha + \beta = \frac{3}{2}$
- The difference of the roots: $d = \alpha - \beta = 2$
Using the formulas for constructing a quadratic equation based on its roots, which is $x^2 - sx + p = 0$, we first need to find the product of the roots $\alpha \beta$.
- Calculate $\alpha \beta$ We can use the equation: $$ \alpha = \beta + 2 $$ Substituting this in the sum: $$ \beta + 2 + \beta = \frac{3}{2} $$ $$ 2\beta + 2 = \frac{3}{2} $$ $$ 2\beta = \frac{3}{2} - 2 $$ $$ 2\beta = \frac{3}{2} - \frac{4}{2} = -\frac{1}{2} $$ $$ \beta = -\frac{1}{4} $$
Now we can find $\alpha$: $$ \alpha = \beta + 2 = -\frac{1}{4} + 2 = \frac{7}{4} $$
-
Determine the product of the roots Now, we calculate $\alpha \beta$: $$ \alpha \beta = \frac{7}{4} \cdot -\frac{1}{4} = -\frac{7}{16} $$
-
Final equation formulation Using the quadratic equation structure: $$ x^2 - \left(\frac{3}{2}\right)x - \left(-\frac{7}{16}\right) = 0 $$ This simplifies to: $$ x^2 - \frac{3}{2}x + \frac{7}{16} = 0 $$
-
Clear the fractions To eliminate the fractions, multiply through by 16: $$ 16x^2 - 24x + 7 = 0 $$
The quadratic equation is
$$ 16x^2 - 24x + 7 = 0 $$
More Information
This quadratic equation has roots that satisfy the given conditions. The roots represent the values of $\alpha$ and $\beta$ found through the system of equations.
Tips
- Misapplying the difference of squares formula. Ensure to factor correctly.
- Not isolating $\alpha + \beta$ properly. Careful algebra is required to avoid errors.
AI-generated content may contain errors. Please verify critical information