Find the number of sides of a regular polygon whose interior angle is 60°.
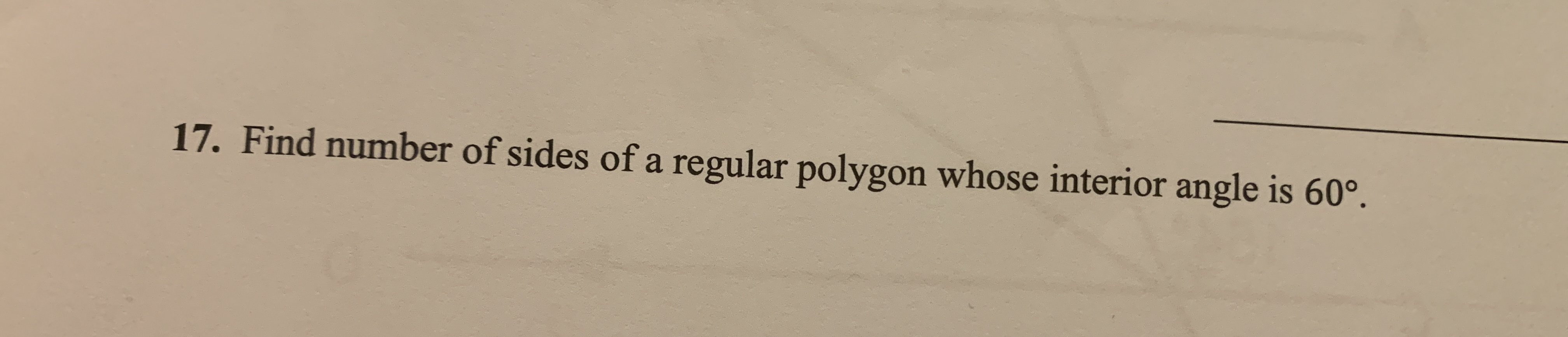
Understand the Problem
The question is asking for the number of sides of a regular polygon given that the interior angle is 60°. This can be solved using the formula for the interior angle of a regular polygon, which is tied to the number of sides.
Answer
3
Answer for screen readers
The number of sides of the polygon is ( n = 3 ).
Steps to Solve
- Use the formula for the interior angle of a polygon
The formula for the interior angle ($I$) of a regular polygon with $n$ sides is given by:
$$ I = \frac{(n - 2) \times 180°}{n} $$
- Substitute the given interior angle
We know that the interior angle $I$ is 60°. Substituting this value into the formula gives:
$$ 60° = \frac{(n - 2) \times 180°}{n} $$
- Multiply both sides by $n$
To eliminate the fraction, multiply both sides by $n$:
$$ 60n = (n - 2) \times 180 $$
- Expand and rearrange the equation
Expanding the equation results in:
$$ 60n = 180n - 360 $$
Rearranging this gives:
$$ 360 = 180n - 60n $$
- Combine like terms
Combining the terms on the right side simplifies to:
$$ 360 = 120n $$
- Solve for $n$
Dividing both sides by 120 gives:
$$ n = \frac{360}{120} = 3 $$
The number of sides of the polygon is ( n = 3 ).
More Information
A polygon with 3 sides is known as a triangle. Interestingly, a regular triangle (equilateral triangle) has exterior angles of 120°, leading to its interior angles all being 60°.
Tips
- Misapplying the interior angle formula by forgetting to account for the division by $n$. This can lead to incorrect solutions.
- Confusing the types of polygons; ensure that the formula used is specifically for regular polygons.
AI-generated content may contain errors. Please verify critical information