Find the nth differential coefficient of sin 2x.
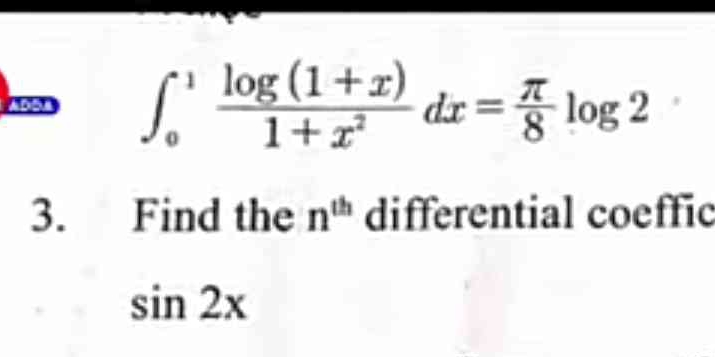
Understand the Problem
The question consists of two parts: first, it provides an integral equation involving logarithmic functions, and second, it asks to find the nth differential coefficient of the function sin 2x. This involves both calculus and differential equations principles.
Answer
The nth differential coefficient of $\sin(2x)$ is given by: $$ \frac{d^n}{dx^n}[\sin(2x)] = 2^n \sin\left(2x + \frac{n\pi}{2}\right) $$
Answer for screen readers
The nth differential coefficient of $\sin(2x)$ is given by:
$$ \frac{d^n}{dx^n}[\sin(2x)] = 2^n \sin\left(2x + \frac{n\pi}{2}\right) $$
Steps to Solve
-
Understanding the nth Derivative Concept
To find the nth differential coefficient of a function, we need to identify a general formula or method for taking derivatives multiple times. For periodic functions like $\sin(2x)$, this can often be simplified. -
Finding the First Derivative
The first derivative of $\sin(2x)$ can be found using the chain rule:
$$ \frac{d}{dx}[\sin(2x)] = 2 \cos(2x) $$ -
Finding the Second Derivative
Now, calculate the second derivative:
$$ \frac{d^2}{dx^2}[\sin(2x)] = \frac{d}{dx}[2 \cos(2x)] = -4 \sin(2x) $$ -
Continuing the Pattern
The third derivative is:
$$ \frac{d^3}{dx^3}[\sin(2x)] = \frac{d}{dx}[-4 \sin(2x)] = -8 \cos(2x) $$
The fourth derivative is:
$$ \frac{d^4}{dx^4}[\sin(2x)] = \frac{d}{dx}[-8 \cos(2x)] = 16 \sin(2x) $$ -
Identifying the nth Derivative Pattern
From the derivatives calculated, we can see a pattern:
- For $n = 1$: $2 \cos(2x)$
- For $n = 2$: $-4 \sin(2x)$
- For $n = 3$: $-8 \cos(2x)$
- For $n = 4$: $16 \sin(2x)$
The pattern appears to alternate between $\sin(2x)$ and $\cos(2x)$, with coefficients that are powers of 2. For even $n$, the derivative has the form $2^n \sin(2x)$, and for odd $n$, it has the form $2^n \cos(2x)$.
- Writing the General Formula
We can summarize the nth derivative as follows:
$$ \frac{d^n}{dx^n}[\sin(2x)] = 2^n \sin\left(2x + \frac{n\pi}{2}\right) $$
This accounts for the alternating nature and scaling factor.
The nth differential coefficient of $\sin(2x)$ is given by:
$$ \frac{d^n}{dx^n}[\sin(2x)] = 2^n \sin\left(2x + \frac{n\pi}{2}\right) $$
More Information
The nth derivative of trigonometric functions like $\sin$ and $\cos$ exhibits periodicity and can be systematically derived. The coefficient involves powers of 2 due to the chain rule applied through multiple derivatives.
Tips
- Forgetting to apply the chain rule correctly can lead to errors in deriving the coefficients.
- Not recognizing the periodic nature of derivatives, causing confusion about the function's behavior for higher derivatives.
AI-generated content may contain errors. Please verify critical information