Find the mean and variance of the standard normal distribution.
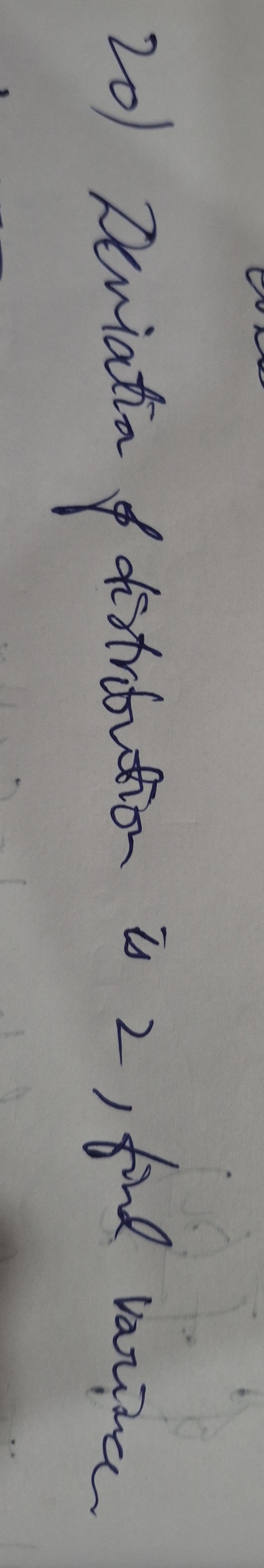
Understand the Problem
The question is asking for the calculation of the mean and variance of a distribution, specifically a standard normal distribution. The high-level approach would involve using the properties of the standard normal distribution to find these values.
Answer
The mean is \( 0 \) and the variance is \( 1 \).
Answer for screen readers
The mean of the standard normal distribution is ( 0 ) and the variance is ( 1 ).
Steps to Solve
- Identify the Mean and Variance of the Standard Normal Distribution
The standard normal distribution, denoted as ( Z ), has specific properties. The mean ( \mu ) is defined as 0, and the variance ( \sigma^2 ) is defined as 1.
- Express Mean and Variance in Mathematical Notation
The mean and variance can be expressed as:
-
Mean:
[ \mu_Z = 0 ] -
Variance:
[ \sigma^2_Z = 1 ]
- Conclude the Analysis
In summary, for a standard normal distribution:
- The mean is 0.
- The variance is 1.
The mean of the standard normal distribution is ( 0 ) and the variance is ( 1 ).
More Information
The standard normal distribution is a special case of the normal distribution. It's widely used in statistics for standardizing scores, allowing for comparisons between different datasets.
Tips
null
AI-generated content may contain errors. Please verify critical information