Find the limit: lim (x->8) of (cube root of x - 2)/(x-8)
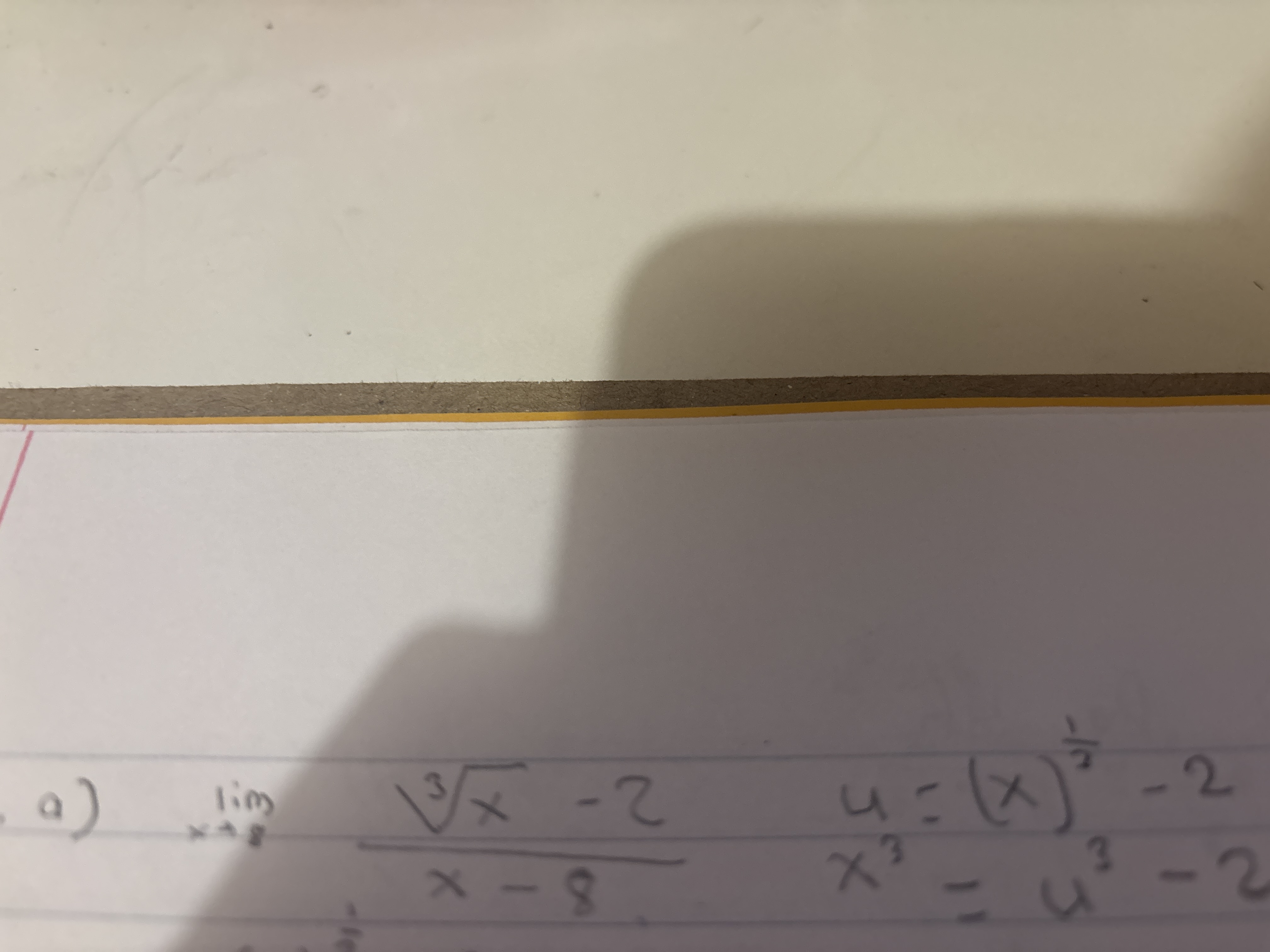
Understand the Problem
The question asks to find the limit of the function (\frac{\sqrt[3]{x} - 2}{x - 8}) as x approaches 8. This is a calculus problem that likely involves L'Hôpital's Rule or algebraic manipulation to resolve the indeterminate form.
Answer
$\frac{1}{12}$
Answer for screen readers
$\frac{1}{12}$
Steps to Solve
-
Check for Indeterminate Form First, we substitute $x = 8$ into the expression to check if we get an indeterminate form: $$ \frac{\sqrt[3]{8} - 2}{8 - 8} = \frac{2 - 2}{0} = \frac{0}{0} $$ Since we have the indeterminate form $\frac{0}{0}$, we can apply L'Hôpital's Rule or manipulate the expression algebraically.
-
Apply L'Hôpital's Rule L'Hôpital's Rule states that if we have an indeterminate form $\frac{0}{0}$ or $\frac{\infty}{\infty}$, then $$ \lim_{x \to c} \frac{f(x)}{g(x)} = \lim_{x \to c} \frac{f'(x)}{g'(x)} $$ provided the limit on the right exists.
-
Find the Derivatives Let $f(x) = \sqrt[3]{x} - 2 = x^{\frac{1}{3}} - 2$ and $g(x) = x - 8$. Then, find their derivatives: $$ f'(x) = \frac{1}{3}x^{\frac{1}{3} - 1} = \frac{1}{3}x^{-\frac{2}{3}} = \frac{1}{3x^{\frac{2}{3}}} $$ $$ g'(x) = 1 $$
-
Apply the Derivatives to the Limit Now, we can apply L'Hôpital's Rule: $$ \lim_{x \to 8} \frac{\sqrt[3]{x} - 2}{x - 8} = \lim_{x \to 8} \frac{\frac{1}{3x^{\frac{2}{3}}}}{1} = \lim_{x \to 8} \frac{1}{3x^{\frac{2}{3}}} $$
-
Evaluate the Limit Substitute $x = 8$ into the expression: $$ \frac{1}{3(8)^{\frac{2}{3}}} = \frac{1}{3(2^3)^{\frac{2}{3}}} = \frac{1}{3(2^2)} = \frac{1}{3(4)} = \frac{1}{12} $$
$\frac{1}{12}$
More Information
The limit of the function as $x$ approaches 8 is $\frac{1}{12}$. L'Hôpital's Rule provides a direct method to evaluate the limit of indeterminate forms.
Tips
A common mistake is incorrectly applying the chain rule when finding the derivative of $\sqrt[3]{x}$. Another mistake could be not recognizing the indeterminate form and attempting to evaluate the limit directly, which would lead to a division by zero error.
AI-generated content may contain errors. Please verify critical information