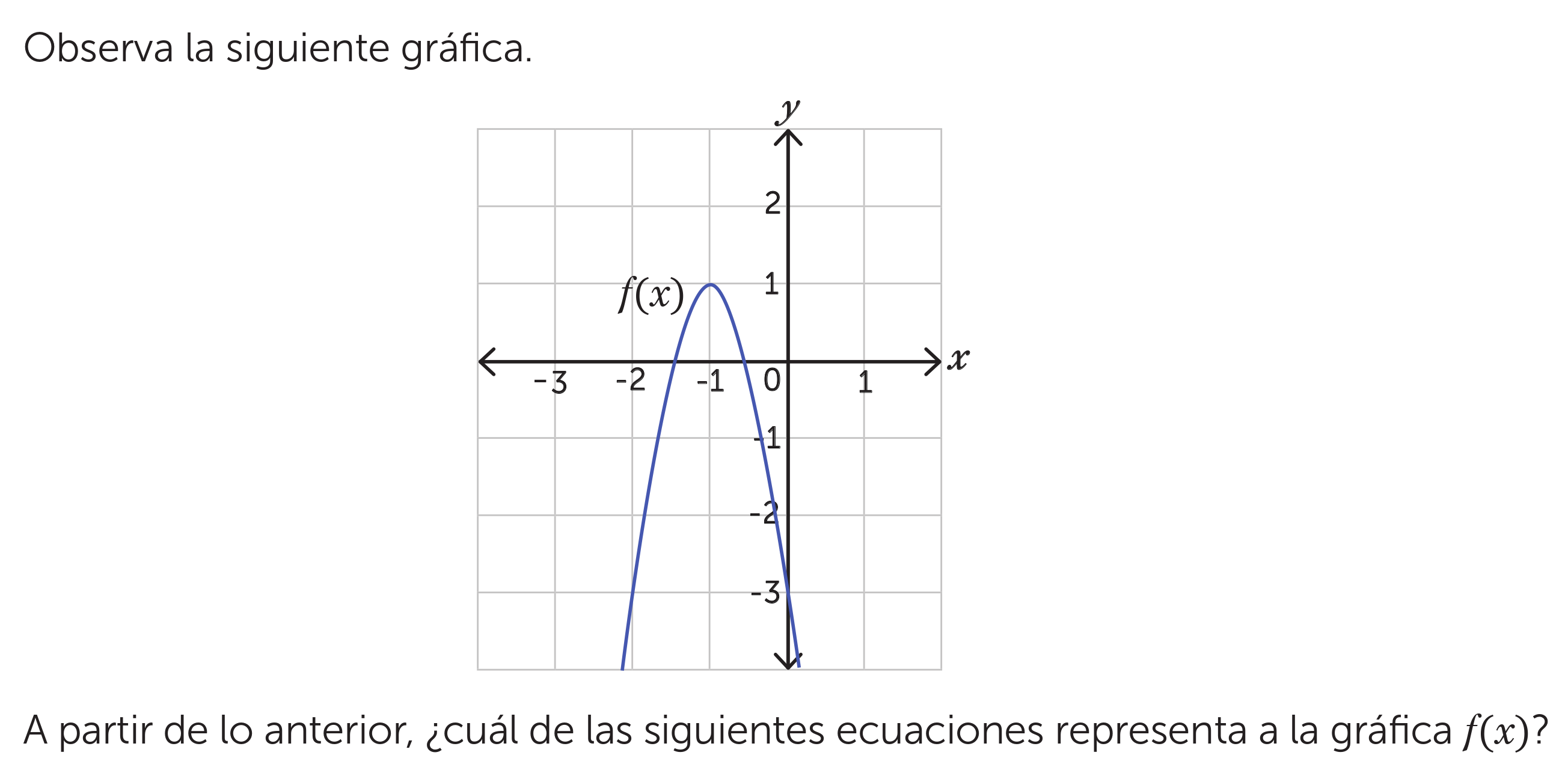
A partir de la gráfica, ¿cuál de las siguientes ecuaciones representa a la gráfica f(x)?
Understand the Problem
La pregunta pide identificar cuál de las ecuaciones dadas representa la gráfica de la función f(x) mostrada en la imagen. Para resolverlo, hay que analizar las características de la parábola, como su vértice, intersecciones con los ejes y concavidad, para determinar la ecuación que mejor se ajusta.
Answer
$f(x) = -4(x + 1)^2 + 1$
Answer for screen readers
$f(x) = -4(x + 1)^2 + 1$
Steps to Solve
- Identify the vertex of the parabola
The vertex of the parabola is located at approximately $(-1, 1)$.
- Consider the general vertex form of a parabola
The general form of a parabola with vertex $(h, k)$ is $f(x) = a(x - h)^2 + k$, where $a$ determines the direction and "width" of the parabola.
- Substitute the vertex coordinates
Since the vertex is $(-1, 1)$, we substitute $h = -1$ and $k = 1$ into the vertex form: $f(x) = a(x - (-1))^2 + 1$, which simplifies to $f(x) = a(x + 1)^2 + 1$.
- Determine the value of $a$ using another point on the graph
We can see the parabola passes through the point $(0, -3)$. Substitute $x = 0$ and $f(x) = -3$ into the equation $f(x) = a(x + 1)^2 + 1$ to solve for $a$:
$-3 = a(0 + 1)^2 + 1$ $-3 = a(1)^2 + 1$ $-3 = a + 1$ $a = -4$
- Write the final equation
Substitute $a = -4$ back into the equation: $f(x) = -4(x + 1)^2 + 1$.
$f(x) = -4(x + 1)^2 + 1$
More Information
The equation represents a parabola that opens downwards (because $a < 0$) with a vertex at $(-1, 1)$. The value of $a = -4$ makes the parabola narrower than the standard parabola $f(x) = x^2$.
Tips
A common mistake might be incorrectly identifying the coordinates of the vertex. Another mistake might be making an error when solving for $a$.
AI-generated content may contain errors. Please verify critical information