Find the limit: lim (x->2) (x^2 - 2x + 1) / (x - 1)
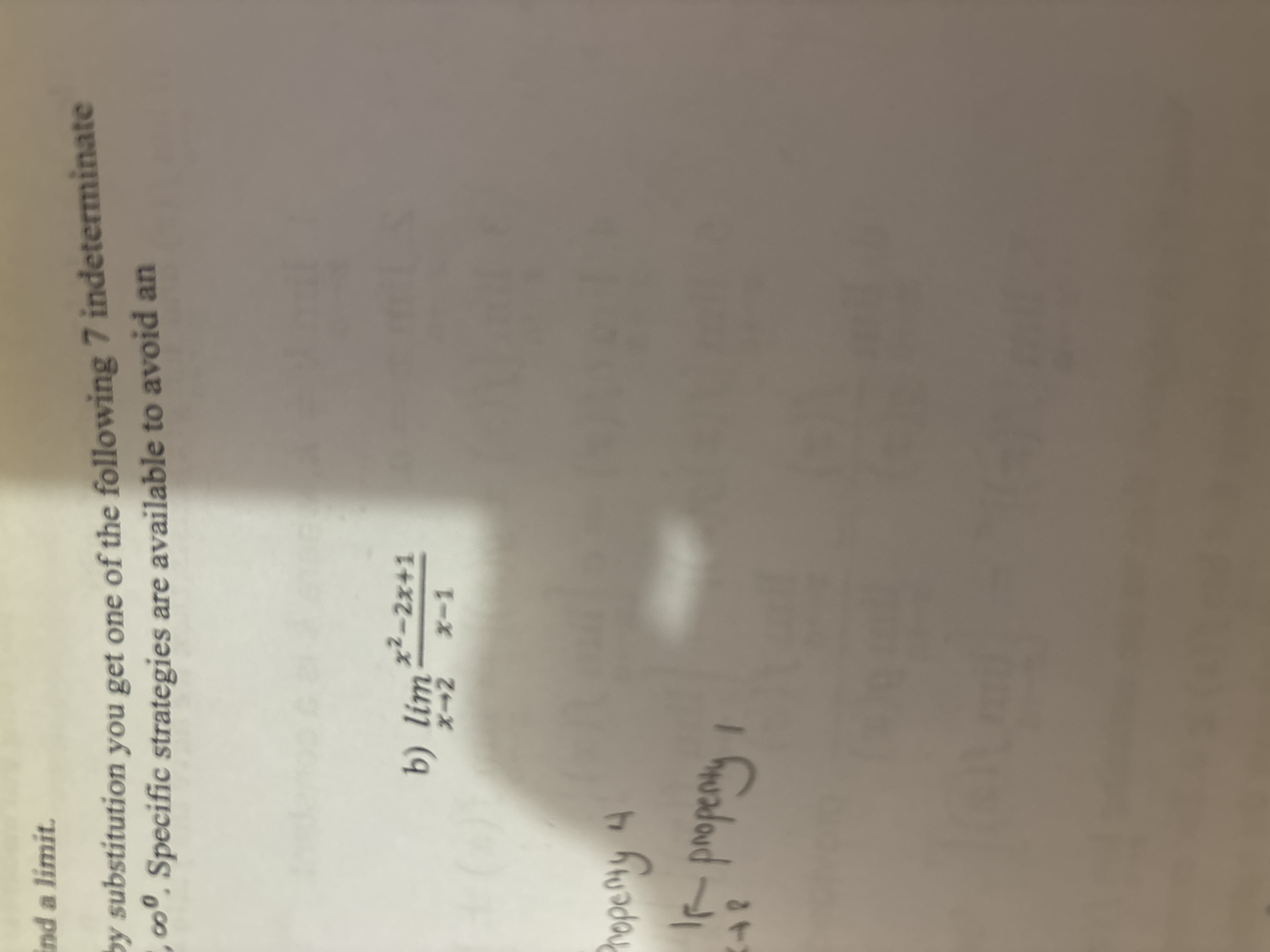
Understand the Problem
The question asks us to evaluate the limit of the function ( \frac{x^2 - 2x + 1}{x-1} ) as ( x ) approaches ( 2 ). To solve this, we can first try to simplify the function and then substitute the value of ( x ) to find the limit.
Answer
$1$
Answer for screen readers
$1$
Steps to Solve
- Factor the numerator
The numerator can be factored as follows: $x^2 - 2x + 1 = (x-1)(x-1) = (x-1)^2$
- Simplify the fraction
Substitute the factored form into the original fraction: $\frac{x^2 - 2x + 1}{x-1} = \frac{(x-1)^2}{x-1} = x-1$
- Evaluate the limit
Now evaluate the limit as $x$ approaches $2$: $\lim_{x \to 2} (x-1) = 2 - 1 = 1$
$1$
More Information
The limit of the given function as $x$ approaches $2$ is $1$. This was found by simplifying the expression inside the limit first, canceling the common factor $(x-1)$, and then substituting $x = 2$ into the simplified expression.
Tips
A common mistake is not simplifying the fraction first. Directly plugging in $x=2$ into the original expression doesn't cause an issue in this particular problem, but simplification makes finding the limit easier and is essential in cases where substitution results in an indeterminate form (like 0/0).
AI-generated content may contain errors. Please verify critical information