Find the length of the indicated side, to the nearest tenth of a metre.
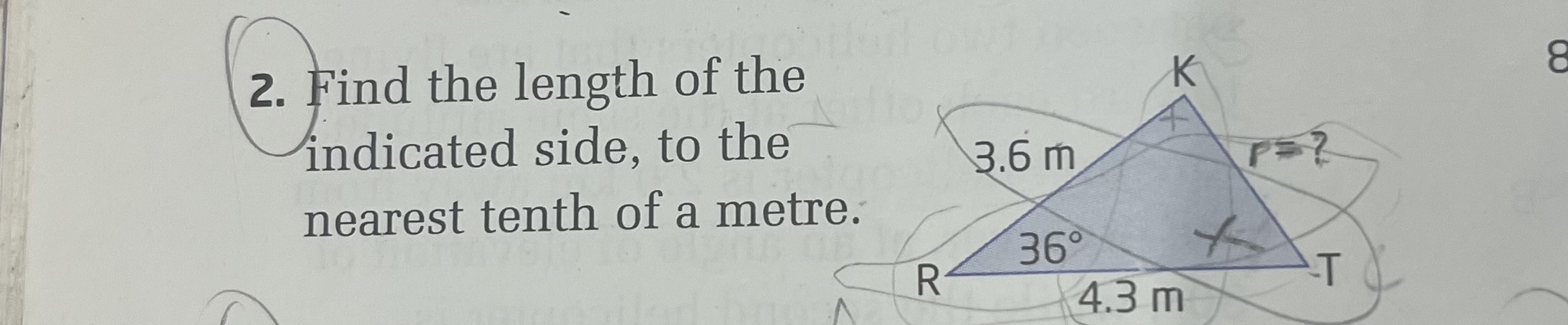
Understand the Problem
The question is asking to calculate the length of the indicated side (labeled 'X') in a triangle, given two sides and an angle. We will likely use trigonometric functions to solve this problem.
Answer
The length of the indicated side \( X \) is approximately \( 2.2 \, \text{m} \).
Answer for screen readers
The length of the indicated side ( X ) is approximately ( 2.2 , \text{m} ).
Steps to Solve
-
Identify the triangle components
In triangle ( RKT ), we have two sides and an angle:
- Side ( RT = 4.3 , \text{m} )
- Side ( RK = 3.6 , \text{m} )
- Angle ( K = 36^\circ )
-
Use the Law of Cosines
To find the side labeled ( X ) (which is ( KT )), we will use the Law of Cosines formula:
$$ c^2 = a^2 + b^2 - 2ab \cdot \cos(C) $$
where:
- ( c ) is the side opposite the angle ( C ) (in this case, ( KT = X ))
- ( a ) and ( b ) are the other two sides (here, ( RT ) and ( RK ))
- ( C ) is the angle ( K )
Thus, our equation becomes:
$$ X^2 = (4.3)^2 + (3.6)^2 - 2 \cdot (4.3) \cdot (3.6) \cdot \cos(36^\circ) $$
-
Calculate the squares of the sides
Calculate ( (4.3)^2 ) and ( (3.6)^2 ):
$$ (4.3)^2 = 18.49 $$
$$ (3.6)^2 = 12.96 $$ -
Calculate the cosine component
Find ( \cos(36^\circ) ) approximately:
$$ \cos(36^\circ) \approx 0.8090 $$
Now substitute values into the equation:
$$ X^2 = 18.49 + 12.96 - 2 \cdot 4.3 \cdot 3.6 \cdot 0.8090 $$
-
Calculate the full expression
Now we can compute the value:
$$ 2 \cdot 4.3 \cdot 3.6 \cdot 0.8090 \approx 26.517 $$
So,
$$ X^2 = 18.49 + 12.96 - 26.517 $$
$$ X^2 = 31.45 - 26.517 = 4.933 $$ -
Take the square root to find X
Finally, take the square root:
$$ X = \sqrt{4.933} \approx 2.22 , \text{m} $$
Rounding to the nearest tenth:
$$ X \approx 2.2 , \text{m} $$
The length of the indicated side ( X ) is approximately ( 2.2 , \text{m} ).
More Information
This problem uses the Law of Cosines, which helps relate the sides and angles of a triangle. It’s especially useful when you have one angle and the two sides adjacent to it.
Tips
- Forgetting to convert degrees to radians: Make sure the calculator is in the correct mode (degrees for this problem).
- Misapplying the formula: Ensure that you are using the correct sides and angle in the Law of Cosines equation.
AI-generated content may contain errors. Please verify critical information